The altitude of an equilateral triangle splits it into two 30-60-90 triangles. The height of the triangle is the longer leg of the 30-60-90 triangle. If the hypotenuse is 8, the longer leg is .

To double check the answer use the Pythagorean Thereom:

Step 1: Locate the side that is opposite the  side..

The shortest side is opposite the  angle. Let's say that this side has length .

Step 2: Recall the ratio of the sides of a  triangle:

From the shortest side, the ratio is .

 is the hypotenuse, which is twice as big as the shortest side..

The ratio of the short side to the hypotenuse is 

We know that in a 30-60=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle.

Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10.

The formula for 

, so  or .

First, we know that in a 30-60-90 triangle,

.

Also, the base is the smallest side times , so in our case it is .

The height is just the smallest side, .

Substituting these values into the formula given for area of a triangle, we obtain the answer .

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

Make sure to round to  places after the decimal.

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

Make sure to round to  places after the decimal.

The flagpole is  feet tall.

You can draw the following right triangle from the information given in the question:

In order to find out how far up the ladder goes, you will need to use sine.

This triangle can exist. Since  is a right angle, we can use the Pythagorean Theorem, where  is the hypoteneuse:

To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25^o, the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w. 

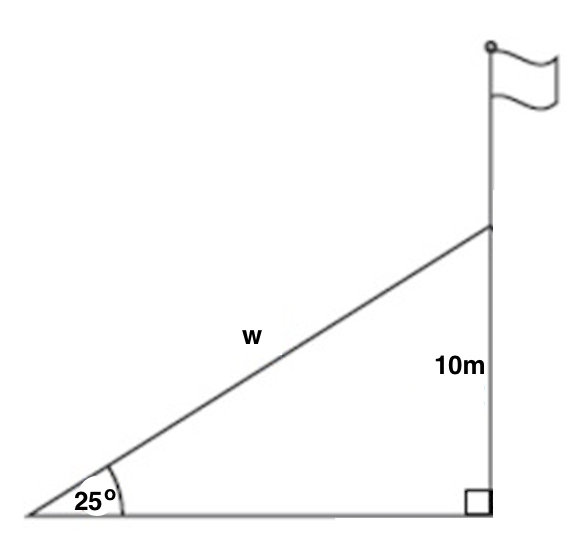
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25^o. 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.

We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:

 (Use a calculator in degree mode to find that  after rounding to two decimal places)

 meters

To solve this problem instead using the cosecant function, we would get:

 (Use a calculator in degree mode to find that  after rounding to two decimal places)

 meters

The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem. 

Please note that the answer choice  is correct based on the Pythagorean Theorem, but does not use all of the provided info to find an exact solution rounded to two decimal places. 

To solve this problem, first set up a diagram that shows all of the info given in the problem. 

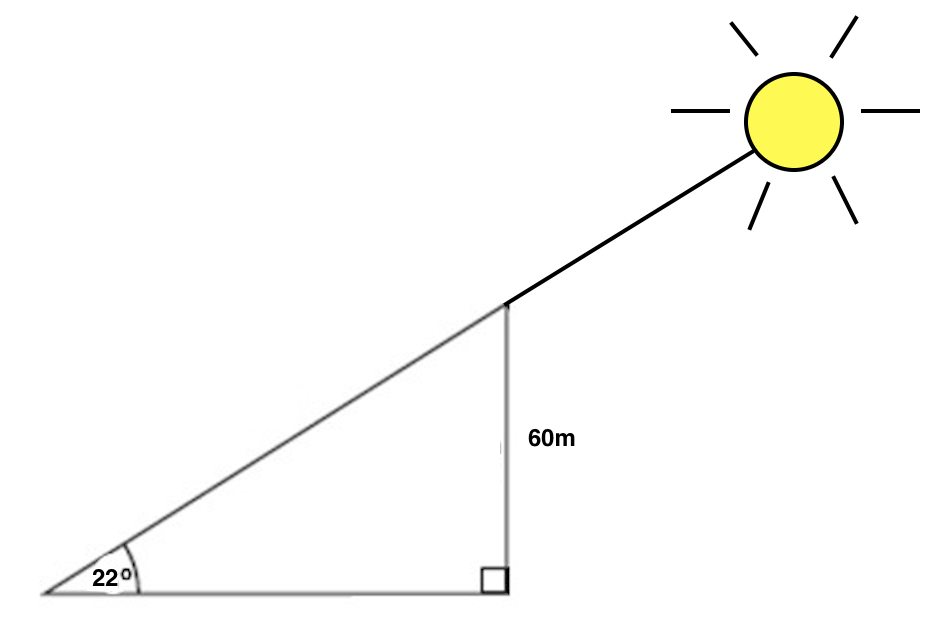
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.

Next, think about which trig functions relate our known angle, 22^o, to the base (or adjacent) and the opposite sides of the triangle. If you thought tangent (or cotangent), you are correct! We know that  and . For simplicity's sake, we'll use tangent to solve this problem. We have: 

 (Use a calculator and round to two places to find that )

 meters

Therefore the shadow cast by the building is 150 meters long.

If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)