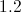We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : How To Add Fractions

In a jar of marbles, $\frac{12}{25}$ of the marbles are red and $\frac{1}{5}$ of the marbles of blue. What fraction of the jar of marbles are red and blue marbles?

Possible Answers:

$\frac{17}{25}$

$\frac{7}{25}$

$\frac{11}{25}$

$\frac{13}{30}$

Correct answer:

$\frac{17}{25}$

Explanation:

To find out what fraction of the jar are red and blue marbles, add $\frac{12}{25}$ and $\frac{1}{5}$ together.

First, you need to convert the fractions so that they have the same denominator. Since is a multiple of , you only need to change one fraction.

$\frac{1}{5}=\frac{5}{25}$

Now, add the fractions together.

$\frac{12}{25}+\frac{1}{5}=\frac{12}{25}+\frac{5}{25}=\frac{17}{25}$

Report an Error

Example Question #2 : How To Add Fractions

Jim baked two batches of cookies. In the first batch, he used $\frac{1}{13}$ cup of sugar. In his second batch, he used $\frac{3}{26}$ cups of sugar. In cups, how much sugar did he use in total?

Possible Answers:

$\frac{9}{26}$

$\frac{5}{26}$

$\frac{4}{39}$

$\frac{1}{26}$

Correct answer:

$\frac{5}{26}$

Explanation:

To find how much sugar he used in total, add $\frac{1}{13}$ and $\frac{3}{26}$ together.

First, make sure that both fractions have the same denominator before you add them. Since is a multiple of , you will need to convert $\frac{1}{13}$ into $\frac{2}{26}$ by multiplying both numerator and denominators by .

Now, add the fractions.

$\frac{1}{13}+\frac{3}{26}=\frac{2}{26}+\frac{3}{26}=\frac{5}{26}$

Report an Error

Example Question #3 : How To Add Fractions

Lucy gave away $\frac{1}{10}$ of her hair ribbons to Megan and $\frac{1}{2}$ of her hair ribbons to Patrice. What fraction of her hair ribbons did Lucy give away?

Possible Answers:

$\frac{2}{5}$

$\frac{3}{5}$

$\frac{2}{10}$

$\frac{1}{6}$

Correct answer:

$\frac{3}{5}$

Explanation:

You will need to add together $\frac{1}{10}$ and $\frac{1}{2}$ .

Since is a multiple of , we can use as the common denominator.

Then, $\frac{1}{2}=\frac{5}{10}$

$\frac{1}{10}+\frac{1}{2}=\frac{1}{10}+\frac{5}{10}=\frac{6}{10}=\frac{3}{5}$

Report an Error

Example Question #8 : How To Add Fractions

Michael ate $\frac{5}{8}$ of a cake for breakfast, and then $\frac{1}{6}$ of the same cake for dinner. How much of the cake did Michael eat?

Possible Answers:

$\frac{11}{24}$

$\frac{5}{14}$

$\frac{19}{24}$

$\frac{3}{7}$

Correct answer:

$\frac{19}{24}$

Explanation:

To figure out how much cake Michael ate, you will need to add the two fractions given in the question.

First, find the common denominator of both fractions and convert them so that they have that denominator.

$\frac{5}{8}=\frac{15}{24}$

$\frac{1}{6}=\frac{4}{24}$

Now, add the fractions.

$\frac{5}{8}+\frac{1}{6}=\frac{15}{24}+\frac{4}{24}=\frac{19}{24}$

Report an Error

Example Question #9 : How To Add Fractions

On a certain game show, the audience is polled. $\frac{29}{100}$ of the audience enjoys playing football, and $\frac{1}{5}$ of the audience enjoys playing basketball. What fraction of the audience enjoys playing football and basketball?

Possible Answers:

$\frac{59}{100}$

$\frac{3}{10}$

$\frac{49}{100}$

$\frac{19}{100}$

Correct answer:

$\frac{49}{100}$

Explanation:

Add the fractions together. In order to do so, you will need to convert $\frac{1}{5}$ so that it shares the same denominator as $\frac{29}{100}$ .

$\frac{1}{5}=\frac{20}{100}$

Now, add the fractions.

$\frac{1}{5}+\frac{29}{100}=\frac{20}{100}+\frac{29}{100}=\frac{49}{100}$

Report an Error

Example Question #1311 : Ssat Upper Level Quantitative (Math)

Solve,

$\frac{2}{13}+\frac{4}{13}=?$

Possible Answers:

$\frac{3}{13}$

$\frac{2}{13}$

$\frac{6}{13}$

$\frac{6}{26}$

Correct answer:

$\frac{6}{13}$

Explanation:

Since the denominators for the fractions are the same, keep the denominator and add the numerators.

$\frac{2}{13}+\frac{4}{13}=\frac{2+4}{13}=\frac{6}{13}$

Report an Error

Example Question #1312 : Ssat Upper Level Quantitative (Math)

On a given week, Jeremy spends $\frac{1}{5}$ of his time working on homework and $\frac{1}{4}$ of his time doing chores. What fraction of his time is spent doing homework and doing chores?

Possible Answers:

$\frac{3}{11}$

$\frac{1}{20}$

$\frac{2}{9}$

$\frac{9}{20}$

Correct answer:

$\frac{9}{20}$

Explanation:

To find how much time Jeremy spends doing his homework and his chores, add together $\frac{1}{5}$ and $\frac{1}{4}$ .

First, convert both fractions so that they have the same denominator.

$\frac{1}{5}=\frac{4}{20}$

$\frac{1}{4}=\frac{5}{20}$

Now, you can add the fractions together.

$\frac{1}{5}+\frac{1}{4}=\frac{4}{20}+\frac{5}{20}=\frac{9}{20}$

Report an Error

Example Question #12 : How To Add Fractions

Solve,

$\frac{3}{4}+\frac{1}{10}=?$

Possible Answers:

$\frac{17}{20}$

$\frac{2}{7}$

$\frac{13}{20}$

$\frac{8}{15}$

Correct answer:

$\frac{17}{20}$

Explanation:

In order to add the fractions, you need to first find a common denominator. For and , the least common denominator is .

$\frac{3}{4}=\frac{15}{20}$

$\frac{1}{10}=\frac{2}{20}$

Then,

$\frac{3}{4}+\frac{1}{10}=\frac{15}{20}+\frac{2}{20}=\frac{17}{20}$

Report an Error

Example Question #1312 : Ssat Upper Level Quantitative (Math)

Give the reciprocal of 0.8.

Possible Answers:

-1.2

-0.8

-1.25

1.2

1.25

Correct answer:

1.25

Explanation:

The reciprocal of a number is the quotient of 1 and that number. Divide 1 by 0.8 by moving the decimal point to the right in each number one place:

$1 \div 0.8 = 10 \div 8 = 1.25$

Report an Error

Example Question #1313 : Ssat Upper Level Quantitative (Math)

Give the reciprocal of 0.75.

Possible Answers:

-1.25

-0.75

$1 \frac{1}{3}$

$-1 \frac{1}{3}$

1.25

Correct answer:

$1 \frac{1}{3}$

Explanation:

The reciprocal of a number is the quotient of 1 and the number.

Divide 1 by 0.75 by moving the decimal point to the right in each number two places:

$1 \div 0.75 = 100 \div 75 = 1 \frac{25}{75} = 1 \frac{1}{3}$

Report an Error

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Dallas Fort Worth, Biology Tutors in Chicago, Physics Tutors in Houston, Biology Tutors in New York City, Math Tutors in New York City, ACT Tutors in New York City, Biology Tutors in Phoenix, LSAT Tutors in Phoenix, Chemistry Tutors in San Diego, Spanish Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in New York City, ACT Courses & Classes in Chicago, ISEE Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Seattle, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Boston, SSAT Courses & Classes in Miami

Popular Test Prep

SAT Test Prep in Chicago, LSAT Test Prep in Phoenix, GRE Test Prep in Dallas Fort Worth, GMAT Test Prep in Seattle, LSAT Test Prep in Atlanta, ISEE Test Prep in Boston, ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Boston, SSAT Test Prep in New York City, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #6 : How To Add Fractions

Example Question #2 : How To Add Fractions

Example Question #3 : How To Add Fractions

Example Question #8 : How To Add Fractions

Example Question #9 : How To Add Fractions

Example Question #1311 : Ssat Upper Level Quantitative (Math)

Example Question #1312 : Ssat Upper Level Quantitative (Math)

Example Question #12 : How To Add Fractions

Example Question #1312 : Ssat Upper Level Quantitative (Math)

Example Question #1313 : Ssat Upper Level Quantitative (Math)

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: