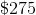Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Fractions

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : Ratios & Proportional Relationships

If it takes Dennis 120 minutes to paint walls, how many minutes does it take him to paint wall?

Possible Answers:

Correct answer:

Explanation:

Divide the time it take Dennis to paint walls by the number of walls he painted to find how long it will take him to paint one wall.

$120\div8=15$

It will take Dennis minutes to paint one wall.

Report an Error

Example Question #2 : Ratios & Proportional Relationships

An arcade charges players $\$1.25$ to play on the machine for minutes. How much money would it cost a player if she wanted to play for an hour?

Possible Answers:

$\$20$

$\$25$

$\$30$

$\$35$

Correct answer:

$\$25$

Explanation:

First, find out how much money it costs to play for one minute.

$1.25\div3=0.41667$

Now, multiply this amount by the number of minutes in an hour to find how much it will cost for the player to play for one hour.

$0.41667\times60=25$

It will cost her $\$25$ to play for one hour.

Report an Error

Example Question #7 : Ratios & Proportional Relationships

If a doctor charges $\$500$ per hour for her services, how much would it cost to hire this doctor for minutes?

Possible Answers:

$\$375$

$\$350$

$\$250$

$\$400$

Correct answer:

$\$375$

Explanation:

First, convert the minutes to hours.

$45\div60=0.75$

Since minutes is 0.75 hours, multiply this by the doctor's hourly rate to find how much it will cost to hire this doctor for minutes.

$500\times0.75=375$

Report an Error

Example Question #3 : Ratios & Proportional Relationships

A dentist charges $\$50$ per hour for the first three hours of an appointment. Any amount of time greater than three hours is charged at $\$25$ per hour. If a patient had a hour long appointment, how much would this appointment cost?

Possible Answers:

$\$325$

$\$300$

$\$275$

$\$250$

Correct answer:

$\$275$

Explanation:

Use the dentist's rate to find how much the first three hours of the appointment will cost.

$50\times 3=150$

Next, use the dentist's second rate to find out how much the last five hours of the appointment will cost.

$25\times5=125$

Now, add these values together to get the cost of the entire appointment.

150+125=275

Report an Error

Example Question #21 : Fractions

On a map, $4\textup{ centimeters}=20\textup{ miles}$ . If two cities are $10\textup{ cm}$ apart on the map, how many miles apart are they in reality?

Possible Answers:

Correct answer:

Explanation:

Set up the following proportion:

$\frac{4}{10}=\frac{20}{x}$ ,

where is the number of miles the cities are apart.

Now, solve for .

4x=200

x=50

The two cities are miles apart.

Report an Error

Example Question #22 : Fractions

Chuck is building a driveway that measures feet by feet. He needs to use pounds of cement for every square foot of driveway. How many pounds of cement does he need to complete the driveway?

Possible Answers:

300

6000

400

500

Correct answer:

6000

Explanation:

First, find the area of the driveway.

$15\times20=300 ft^2$

Since it takes pounds of cement per square feet,

$300\times20=6000$ pounds will be needed to complete the driveway.

Report an Error

Example Question #11 : Ratios & Proportional Relationships

Joanna can finish math problems in minutes. How many minutes would it take her to finish math problems?

Possible Answers:

$300\textup { min}$

$315\textup { min}$

$245\textup { min}$

$270\textup { min}$

Correct answer:

$270\textup { min}$

Explanation:

First, find out how long it will take her to finish math problem.

$45\div10=4.5$

Since it takes Joanna 4.5 minutes to finish one problem, multiply this number by the amount of questions she needs to do.

$4.5\times60=270$

It will take her 270 minutes to finish questions.

Report an Error

Example Question #1134 : Gre Quantitative Reasoning

A pie is made up of $\frac{1}{9}$ crust, $\frac{1}{3}$ apples, and $\frac{1}{4}$ sugar, and the rest is jelly. What is the ratio of crust to jelly?

Possible Answers:

11:36

1:4

3:10

4:11

11:3

Correct answer:

4:11

Explanation:

A pie is made up of $\frac{1}{9}$ crust, $\frac{1}{3}$ apples, $\frac{1}{4}$ sugar, and the rest is jelly. What is the ratio of crust to jelly?

To compute this ratio, you must first ascertain how much of the pie is jelly. This is:

$1-\frac{1}{4}-\frac{1}{3}-\frac{1}{9}$

Begin by using the common denominator :

$1-\frac{1}{4}-\frac{1}{3}-\frac{1}{9}=\frac{36}{36}-\frac{9}{36}-\frac{12}{36}-\frac{4}{36}$

$\frac{36}{36}-\frac{9}{36}-\frac{12}{36}-\frac{4}{36}=\frac{11}{36}$

So, the ratio of crust to jelly is:

$\frac{1}{9}:\frac{11}{36}$

This can be written as the fraction:

$\frac{\frac{1}{9}}{\frac{11}{36}}=\frac{1}{9}*\frac{36}{11}=\frac{4}{11}$ , or 4:11

Report an Error

Example Question #21 : Fractions

In a solution, $\frac{1}{3}$ of the fluid is water, $\frac{1}{5}$ is wine, and $\frac{7}{15}$ is lemon juice. What is the ratio of lemon juice to water?

Possible Answers:

7:8

7:3

5:7

3:5

7:5

Correct answer:

7:5

Explanation:

This problem is really an easy fraction division. You should first divide the lemon juice amount by the water amount:

$\frac{lemon\:juice}{water}=\frac{\frac{7}{15}}{\frac{1}{3}}$

Remember, to divide fractions, you multiply by the reciprocal:

$\frac{\frac{7}{15}}{\frac{1}{3}} = \frac{7}{15}*3=\frac{7}{5}$

This is the same as saying:

7:5

Report an Error

Example Question #45 : Proportion / Ratio / Rate

If $x=\frac{11}{100}$ and $y=\frac{15}{8}$ , what is the ratio of to ?

Possible Answers:

121 : 800

165:800

15:200

45 : 191

22:375

Correct answer:

22:375

Explanation:

To find a ratio like this, you simply need to make the fraction that represents the division of the two values by each other. Therefore, we have:

$x:y=\frac{\frac{11}{100}}{\frac{15}{8}}$

Recall that division of fractions requires you to multiply by the reciprocal:

$\frac{\frac{11}{100}}{\frac{15}{8}} = \frac{11}{100}*\frac{8}{15}=\frac{11}{25}*\frac{2}{15}$ ,

which is the same as:

$\frac{22}{375}$

This is the same as the ratio:

22:375

Report an Error

View SSAT- Upper Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Upper Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SSAT- Upper Level Tutors

Theodore
Certified Tutor

Harvard University, Bachelor in Arts, Folklore Studies. HoHoKus-Hackensack School of Business and Medical Sciences, Doctor of...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Chicago, Math Tutors in Phoenix, Calculus Tutors in Washington DC, Chemistry Tutors in Dallas Fort Worth, Reading Tutors in Houston, Math Tutors in Atlanta, Algebra Tutors in Washington DC, Biology Tutors in Boston, Algebra Tutors in Miami, Spanish Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in San Diego, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Diego, MCAT Courses & Classes in Boston, ACT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in New York City, ACT Courses & Classes in New York City, LSAT Courses & Classes in Chicago, GRE Courses & Classes in Boston, LSAT Courses & Classes in New York City

Popular Test Prep

SSAT Test Prep in Phoenix, LSAT Test Prep in Chicago, SAT Test Prep in Houston, ISEE Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in Phoenix, SSAT Test Prep in Seattle, SAT Test Prep in Atlanta, SAT Test Prep in Denver, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Fractions

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #5 : Ratios & Proportional Relationships

Example Question #2 : Ratios & Proportional Relationships

Example Question #7 : Ratios & Proportional Relationships

Example Question #3 : Ratios & Proportional Relationships

Example Question #21 : Fractions

Example Question #22 : Fractions

Example Question #11 : Ratios & Proportional Relationships

Example Question #1134 : Gre Quantitative Reasoning

Example Question #21 : Fractions

Example Question #45 : Proportion / Ratio / Rate

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: