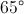All SSAT Upper Level Math Resources
Example Questions
Example Question #223 : Geometry

Figure NOT drawn to scale.
If 


The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so
Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle
If the vertex angle of an isoceles triangle is 
In an isosceles triangle, the base angles are the same. Also, the three angles of a triangle add up to 
So, subtract the vertex angle from 

Because there are two base angles you divide 


Example Question #2 : How To Find An Angle In An Acute / Obtuse Triangle

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Which of the following could be a measure of 
All of the other choices give a possible measure of 
The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

We also have the following constraints:
Then, by the addition property of inequalities,
Therefore, the measure of 

Example Question #3 : How To Find An Angle In An Acute / Obtuse Triangle

Refer to the above diagram.
Which of the following could be a measure of 
All of the other responses are correct.
All of the other responses are correct.
The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so
or
Therefore, the maximum value of 


The minimum value of 


Therefore,
Since all of the choices fall in this range, all are possible measures of 
Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle
Find the angle measurement of 

All the angles in a triangle must add up to 
Example Question #111 : Properties Of Triangles
Find the angle measurement of 

All the angles in a triangle must add up to
Example Question #112 : Properties Of Triangles
Find the angle measurement of 

All the angles in a triangle must add up to 
Example Question #113 : Properties Of Triangles
An isosceles triangle has an angle whose measure is 
What could be the measures of one of its other angles?
(a)
(b)
(c)
(a) or (c) only
(b) only
(a) only
(c) only
(a), (b), or (c)
(a), (b), or (c)
By the Isosceles Triangle Theorem, an isosceles triangle has two congruent interior angles. There are two possible scenarios if one angle has measure 
Scenario 1: The other two angles are congruent to each other. The degree measures of the interior angles of a triangle total 

This makes (b) a possible answer.
Scenario 2: One of the other angles measures 

making (a) a possible answer. Therefore, the correct choice is (a), (b), or (c).
Example Question #114 : Properties Of Triangles
One of the interior angles of a scalene triangle measures 
A scalene triangle has three sides of different measure, so, by way of the Converse of the Isosceles Triangle Theorem, each angle is of different measure as well. We can therefore eliminate 
Also, if the triangle also has a 


Therefore, the triangle has two angles that measure the same, and 
Similarly, if the triangle also has a 


The triangle has two angles that measure 


an impossible situation since angle measures must be positive.
The remaining possibility is 

The three angles have different measures, so the triangle is scalene. 
Example Question #5 : How To Find An Angle In An Acute / Obtuse Triangle
Given: 







Above is the figure described.
The measures of the interior angles of a triangle total 

Since 
and
All SSAT Upper Level Math Resources