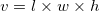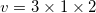All SSAT Upper Level Math Resources
Example Questions
Example Question #54 : Volume Of A Three Dimensional Figure
Find the volume of a regular tetrahedron with side lengths of 
Use the following formula to find the volume of a regular tetrahedron:
Now, plug in the given side length.
Example Question #55 : Volume Of A Three Dimensional Figure
Find the volume of a regular tetrahedron with side lengths of 
Use the following formula to find the volume of a regular tetrahedron:
Now, plug in the given side length.
Example Question #51 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume of a given prism 



Substituting in our known values:
Example Question #52 : Volume Of A Three Dimensional Figure
Find the volume of a circular prism with a base radius of 

The volume of a given prism 



Substituting in our known values:
Example Question #53 : Volume Of A Three Dimensional Figure
A triangular prism has a triangle base length of 


Not enough information provided
The volume of a given prism 





Therefore, we can substitute the base area equation into the equation for the volume of a prism:
Substituting in our known values:
Example Question #51 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume 



Example Question #52 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume 



Example Question #671 : Geometry
What is the volume of the shape below?
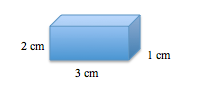
The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #671 : Geometry
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #1 : How To Find The Volume Of A Prism
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Certified Tutor
All SSAT Upper Level Math Resources