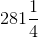SSAT Upper Level Math : Geometry
Study concepts, example questions & explanations for SSAT Upper Level Math
All SSAT Upper Level Math Resources
Example Questions
Example Question #7 : How To Find The Volume Of A Polyhedron
Find the volume of a regular hexahedron with a side length of 
A regular hexahedron is another name for a cube.
To find the volume of a cube,
Plugging in the information given in the question gives
Example Question #8 : How To Find The Volume Of A Polyhedron
Find the volume of a regular octahedron with side lengths of 
Use the following formula to find the volume of a regular octahedron:
Plugging in the information from the question,
Example Question #9 : How To Find The Volume Of A Polyhedron
Find the volume of a prism that has a right triangle base with leg lengths of 
To find the volume of a prism, multiply the area of the base by the height.
Example Question #651 : Geometry
Find the volume of a regular hexagonal prism that has a height of 
The formula to find the volume of a hexagonal prism is
Plugging in the values given by the question will give
Example Question #652 : Geometry
Find the volume of a regular tetrahedron that has side lengths of 
The formula to find the volume of a tetrahedron is
Plugging in the information given by the question gives
Example Question #1 : How To Find The Volume Of A Tetrahedron
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
Give its volume.
A tetrahedron is a triangular pyramid and can be looked at as such.
Three of the vertices - 
Its base is 10 and its height is 18, so its area is
The fourth vertex is off the 
Example Question #1 : How To Find The Volume Of A Tetrahedron
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
What is the volume of this tetrahedron?
The correct answer is not among the other responses.
The tetrahedron looks like this:
This is a triangular pyramid, and we can consider 
The volume of the tetrahedron is one third the product of its base and its height, the latter of which is 15. Therefore,
Example Question #2 : How To Find The Volume Of A Tetrahedron
Above is the base of a triangular pyramid, which is equilateral. The height of the pyramid is equal to the perimeter of its base. In terms of 
By the 30-60-90 Theorem, 
The area of the triangular base is half the product of its base and its height:
The height of the pyramid is equal to the perimeter, so it will be three times 
The volume of the pyramid is one third the product of this area and the height of the pyramid:
Example Question #3 : How To Find The Volume Of A Tetrahedron
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates
where
Give its volume in terms of 
The tetrahedron looks like this:
This is a triangular pyramid, and we can consider
The volume of the tetrahedron is one third the product of its base and its height. Therefore,
After some rearrangement:
Example Question #5 : How To Find The Volume Of A Tetrahedron
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates
where
Give its volume in terms of 
The tetrahedron looks like this:
This is a triangular pyramid, and we can consider 
The volume of the tetrahedron is one third the product of its base area 
Certified Tutor
All SSAT Upper Level Math Resources
