All SSAT Upper Level Math Resources
Example Questions
Example Question #151 : Geometry
The volume of a sphere is 1000 cubic inches. What is the diameter of the sphere.
The volume of a sphere is:
Where 


So we can get:
Example Question #1 : Volume Of A Three Dimensional Figure
A sphere has a diameter of 





To find the volume of a sphere, use the following formula:


Now, because we are given the diameter of the sphere, divide that value in half to find the radius.

Now, plug this value into the volume equation.


Example Question #6 : Volume Of A Three Dimensional Figure
What is the volume of a sphere with a diameter of 
Write the formula for the volume of the sphere.
The radius is half the diameter, which is five. Substitute the value.
Example Question #621 : Geometry
What is the volume of a sphere with diameter 12 feet?
None of the other answers are correct
The radius of the sphere is half the diameter, or 6 feet; use the formula

Setting 
Example Question #621 : Geometry
Chestnut wood has a density of about 
First, convert the dimensions to cubic centimeters by multiplying by 


Its volume is found by using the formula and the converted height and radius.
Now multiply this by 
Finally, convert the answer to kilograms.
Example Question #162 : Geometry
A cone has the height of 4 meters and the circular base area of 4 square meters. If we want to fill out the cone with water (density = 
6333
The volume of a cone is:
where 

As the circular base area is 
where 
We know that density is defined as mass per unit volume or:
Where 


Example Question #1 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
The vertical height (or altitude) of a right cone is 


The volume of a cone is:
where 

Example Question #161 : Geometry
A right cone has a volume of 



The volume of a cone is given by:
where 

Example Question #1 : How To Find The Volume Of A Cone
A cone has a diameter of 

First, divide the diameter in half to find the radius.
Now, use the formula to find the volume of the cone.
Example Question #2 : How To Find The Volume Of A Cone
A cone has a radius of 

The volume of a cone is given by the formula:
Now, plug in the values of the radius and height to find the volume of the given cone.
All SSAT Upper Level Math Resources






























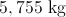
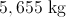























![2\sqrt[3]{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/139528/gif.latex)

![\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/139525/gif.latex)
![\sqrt[3]{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/139524/gif.latex)


![\Rightarrow 8\pi=4\pi t^3\Rightarrow t^3=2\Rightarrow t=\sqrt[3]{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/139604/gif.latex)

















