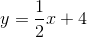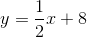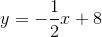Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Coordinate Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #384 : Geometry

What are the coordinates for point L?

Graph11

Possible Answers:

(2, 5)

(-5, 2)

(5, 2)

(2, -5)

Correct answer:

(2, -5)

Explanation:

Find the x-coordinate by going right on the horizontal x-axis until you come across the line that is directly above the point. The x-coordinate is .

Now, continue down until you reach the point and look across to the vertical y-axis. The y-coordinate is .

(2, -5) are the coordinates for point L.

Report an Error

Example Question #601 : Ssat Upper Level Quantitative (Math)

What are the coordinates for point M?

Graph12

Possible Answers:

(-7, -4)

(-4, 7)

(7, 4)

(4, 7)

Correct answer:

(7, 4)

Explanation:

Find the x-coordinate by going right on the horizontal x-axis until you come across the line that is directly under the point. The x-coordinate is .

Now, continue up until you reach the point and look across to the vertical y-axis. The y-coordinate is .

(7, 4) are the coordinates for point M.

Report an Error

Example Question #602 : Ssat Upper Level Quantitative (Math)

What are the coordinates for point K?

Graph10

Possible Answers:

(6, 3)

(-6, 3)

(-3, -6)

(-6, -3)

Correct answer:

(-6, -3)

Explanation:

Find the x-coordinate by going left on the horizontal x-axis until you come across the line that is above the point. The x-coordinate is .

Now, continue down until you reach the point and look across to the vertical y-axis. The y-coordinate is .

(-6, -3) are the coordinates for point K.

Report an Error

Example Question #1 : How To Graph A Function

Line

Refer to the above red line. A line is drawn perpendicular to that line, and with the same -intercept. Give the equation of that line in slope-intercept form.

Possible Answers:

$y = \frac{1}{2}x - 4$

$y = \frac{1}{2}x + 8$

$y = - \frac{1}{2}x + 4$

$y = - \frac{1}{2}x + 8$

$y = \frac{1}{2}x + 4$

Correct answer:

$y = - \frac{1}{2}x + 8$

Explanation:

First, we need to find the slope of the above line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-4, y_{1}=x_{2}= 0, y_{2}=8$ :

$m = \frac{8-0}{0-(-4)} = \frac{8}{4} = 2$

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be $m = -\frac{1}{2}$ . Since we want this line to have the same -intercept as the first line, which is the point (0,8) , we can substitute $m = -\frac{1}{2}$ and b = 8 in the slope-intercept form:

y = mx + b

$y = - \frac{1}{2}x + 8$

Report an Error

Example Question #63 : Graphing

Axes

Refer to the above diagram. If the red line passes through the point $\left ( N, 4\right )$ , what is the value of ?

Possible Answers:

N = -5

$N = -4\frac{2}{3}$

$N = -3\frac{1}{3}$

$N= -1\frac{1}{3}$

$N = -7\frac{1}{3}$

Correct answer:

$N = -4\frac{2}{3}$

Explanation:

One way to answer this is to first find the equation of the line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18$ :

$m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3$

The line has slope 3 and -intercept (0,18) , so we can substitute m = 3, b = 18 in the slope-intercept form:

y = mx+b

y = 3x+18

Now substitute 4 for and for and solve for :

4= 3N+18

-14 =3N

$N = -\frac{14}{3}= -4\frac{2}{3}$

Report an Error

Example Question #381 : Geometry

Multiply:

$\left (7 - 2i \right )\left (7 - 3i \right )$

Possible Answers:

49 + 6i

55 +7i

43 -35i

55 -35i

43 -7i

Correct answer:

43 -35i

Explanation:

FOIL the product out:

$\left (7 - 2i \right )\left (7 - 3i \right )$

$= 7 \cdot 7 - 7 \cdot 3i - 7 \cdot 2i + 2i \cdot 3i$

$= 49 -21i - 14i + 6 i^{2}$

= 49 -21i - 14i + 6 (-1)

= 49 -6 -21i - 14i

= 43 -35i

Report an Error

Example Question #1 : How To Graph Complex Numbers

Simplify:

$\left ( 8 - 3i\right ) ^{2}$

Possible Answers:

55 +48i

73- 48i

55 - 48i

Correct answer:

55 - 48i

Explanation:

Use the square of a binomial pattern to multiply this:

$\left ( 8 - 3i\right ) ^{2}$

$= 8 ^{2}- 2 \cdot8\cdot3i + \left ( 3i\right )^{2}$

$= 64- 48i + 3^{2}i^{2}$

= 64- 48i + 9 (-1)

= 64-9 - 48i

= 55 - 48i

Report an Error

Example Question #392 : Geometry

Multiply:

(1.1 + 0.6i )(1.1 - 0.6i )

Possible Answers:

1.21 - 0.36i

1.57 - 1.32i

0.85 + 1.32i

0.85

1.57

Correct answer:

1.57

Explanation:

This is a product of an imaginary number and its complex conjugate, so it can be evaluated using this formula:

$\left (a + bi \right )\left (a -bi \right ) = a^{2} + b ^{2}$

$\left (1.1 + 0.6i \right )\left (1.1 -0.6 i \right ) = 1.1^{2} + 0.6 ^{2} = 1.21 + 0.36 = 1.57$

Report an Error

Example Question #613 : Ssat Upper Level Quantitative (Math)

Multiply:

$\left (5 - 3i \right )\left (5 +3i \right )$

Possible Answers:

25 -9i

34 +30i

16 -30i

Correct answer:

Explanation:

This is a product of an imaginary number and its complex conjugate, so it can be evaluated using this formula:

$\left (a - bi \right )\left (a +bi \right ) = a^{2} + b ^{2}$

$\left (5 - 3i \right )\left (5 +3i \right ) = 5 ^{2} + 3 ^{2}= 25 + 9 = 34$

Report an Error

Example Question #5 : How To Graph Complex Numbers

Define an operation as follows:

For all complex numbers a,b ,

$a*b = a ^{5}-b^{3}$

Evaluate $\left (2 i \right )* \left (3i \right )$

Possible Answers:

-27+32i

27 -32i

32 - 27i

59i

Correct answer:

59i

Explanation:

$a*b = a ^{5}-b^{3}$

$\left (2 i \right )* \left (3i \right ) = \left (2 i \right ) ^{5}-\left (3i \right ) ^{3}$

$= 2^{5} i^{5} - 3^{3} i ^{3}$

$= 32\cdot i^{4} \cdot i - 27 \cdot (-i )$

$= 32\cdot 1 \cdot i +27 i$

= 32 i +27 i

= 59 i

Report an Error

View SSAT- Upper Level Tutors

Meg, M.Ed.
Certified Tutor

The University of Tennessee, Bachelor of Science, Hospitality Administration and Management. Lincoln Memorial University, Mas...

View SSAT- Upper Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Upper Level Tutors

Yawen
Certified Tutor

Oregon State University, Masters in Business Administration, Business Administration and Management. Oregon State University,...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Denver, Spanish Tutors in Atlanta, SSAT Tutors in Chicago, Reading Tutors in Phoenix, Chemistry Tutors in Dallas Fort Worth, English Tutors in Philadelphia, Reading Tutors in Chicago, Chemistry Tutors in Atlanta, Statistics Tutors in San Diego, Spanish Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Washington DC, LSAT Courses & Classes in Denver, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Phoenix, Spanish Courses & Classes in Seattle, GRE Courses & Classes in San Diego, Spanish Courses & Classes in New York City, SSAT Courses & Classes in Chicago, ACT Courses & Classes in Chicago

Popular Test Prep

ISEE Test Prep in Houston, GMAT Test Prep in Atlanta, GMAT Test Prep in Philadelphia, GMAT Test Prep in San Diego, SSAT Test Prep in Miami, SAT Test Prep in Boston, SSAT Test Prep in Phoenix, GMAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Washington DC, ACT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Coordinate Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #384 : Geometry

Example Question #601 : Ssat Upper Level Quantitative (Math)

Example Question #602 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Graph A Function

Example Question #63 : Graphing

Example Question #381 : Geometry

Example Question #1 : How To Graph Complex Numbers

Example Question #392 : Geometry

Example Question #613 : Ssat Upper Level Quantitative (Math)

Example Question #5 : How To Graph Complex Numbers

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: