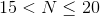All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : Simplifying Fractions
Rewrite the mixed fraction 





The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator. The new denominator is the same as the old one. Therefore,

Multiply the numerator and the denominator: 
a three-digit number.
Example Question #2 : Simplifying Fractions
Reduce 


Add the numerator and the denominator:
The correct response is therefore 
Example Question #3 : How To Simplify A Fraction
Consider a fraction 

I)
II)
III)
IV)
The prime factorization of 



We can immediately tell that 115 is the only multiple of 5, so we test the other numbers to see if there is a multiple of 13. We soon see that

115 and 117 are the only values of 
Example Question #343 : Number Concepts And Operations
Reduce the fraction 


Multiply the numerator and the denominator:
The product is a three-digit number.
Example Question #3 : Simplifying Fractions
Put the fraction in the simplest form.
To put a fraction in simplest form, keep dividing the numerator and denominator by the same number until you cannot go any further.
Example Question #4 : Simplifying Fractions
Put the fraction in simplest form.
To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.
Example Question #5 : Simplifying Fractions
Put the fraction in simplest form.
To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.
Example Question #6 : Simplifying Fractions
Put the fraction in simplest form.
To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.
Example Question #7 : Simplifying Fractions
Put the fraction in simplest form.
To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.
Example Question #8 : Simplifying Fractions
Put the fraction in simplest form.
To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.
All SSAT Upper Level Math Resources