All SSAT Upper Level Math Resources
Example Questions
Example Question #511 : Ssat Upper Level Quantitative (Math)

Give the equation of the above ellipse.
The equation of the ellipse with center , horizontal axis of length , and vertical axis of length is
The ellipse has center , horizontal axis of length 8, and vertical axis of length 16. Therefore,
, , and .
The equation of the ellipse is
Example Question #512 : Ssat Upper Level Quantitative (Math)

Give the equation of the above ellipse.
The equation of the ellipse with center , horizontal axis of length , and vertical axis of length is
The ellipse has center , horizontal axis of length 10, and vertical axis of length 6. Therefore,
, , and .
The equation of the ellipse is
Example Question #513 : Ssat Upper Level Quantitative (Math)

Give the equation of the above ellipse.
The equation of the ellipse with center , horizontal axis of length , and vertical axis of length is
The ellipse has center , horizontal axis of length 8, and vertical axis of length 6. Therefore,
, , and .
The equation of the ellipse is
Example Question #514 : Ssat Upper Level Quantitative (Math)
The -intercept and the only -intercept of a vertical parabola on the coordinate plane coincide with the -intercept and the -intercept of the line of the equation . Give the equation of the parabola.
Insufficient information is given to determine the equation.
To find the -intercept, that is, the point of intersection with the -axis, of the line of equation , set and solve for :
The -intercept is .
The -intercept can be found by doing the opposite:
The -intercept is .
The parabola has these intercepts as well. Also, since the vertical parabola has only one -intercept, that point doubles as its vertex as well.
The equation of a vertical parabola, in vertex form, is
,
where is the vertex. Set :
for some real . To find it, use the -intercept, setting
The parabola has equation , which is rewritten as
Example Question #515 : Ssat Upper Level Quantitative (Math)
An ellipse on the coordinate plane has as its center the point . It passes through the points and . Give its equation.
Insufficient information is given to determine the equation.
The equation of the ellipse with center , horizontal axis of length , and vertical axis of length is
The center is , so and .
To find , note that one endpoint of the horizontal axis is given by the point with the same -coordinate through which it passes, namely, . Half the length of this axis, which is , is the difference of the -coordinates, so . Similarly, to find , note that one endpoint of the vertical axis is given by the point with the same -coordinate through which it passes, namely, . Half the length of this axis, which is , is the difference of the -coordinates, so .
The equation is
or
.
Example Question #516 : Ssat Upper Level Quantitative (Math)
An ellipse passes through points .
Give its equation.
The equation of the ellipse with center , horizontal axis of length , and vertical axis of length is
and are the endpoints of a horizontal line segment with midpoint
, or
and length .
and are the endpoints of a vertical line segment with midpoint
, or
and length
Because their midpoints coincide, these are the endpoints of the horizontal axis and vertical axis, respectively, of the ellipse, and the common midpoint is the center.
Therefore,
and ;
and ; consequently and .
The equation of the ellipse is
, or
Example Question #517 : Ssat Upper Level Quantitative (Math)
A horizontal parabola on the coordinate plane as its only -intercept; its -intercept is .
Give its equation.
Insufficient information is given to determine the equation.
If a horizontal parabola has only one -intercept, which here is , that point doubles as its vertex as well.
The equation of a horizontal parabola, in vertex form, is
,
where is the vertex. Set :
To find , use the -intercept, setting :
The equation, in vertex form, is . In standard form:
Example Question #518 : Ssat Upper Level Quantitative (Math)
A horizontal parabola on the coordinate plane has vertex ; one of its -intercepts is .
Give its equation.
Insufficient information is given to determine the equation.
The equation of a horizontal parabola, in vertex form, is
,
where is the vertex. Set :
To find , use the known -intercept, setting :
The equation, in vertex form, is ; in standard form:
Example Question #519 : Ssat Upper Level Quantitative (Math)
A vertical parabola on the coordinate plane has -intercepts and , and passes through .
Give its equation.
Insufficient information is given to determine the equation.
A horizontal parabola which passes through and has as its equation
.
To find , substitute the coordinates of the third point, setting :
The equation is therefore , which is, in standard form:
Example Question #520 : Ssat Upper Level Quantitative (Math)
A vertical parabola on the coordinate plane has -intercepts and , and passes through .
Give its equation.
A vertical parabola which passes through and has as its equation
To find , substitute the coordinates of the third point, setting :
The equation is ; expand to put it in standard form:
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources


































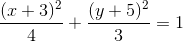






























































































































![x = a[y-(-6)]^{2}+ (-3)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/350996/gif.latex)





















































