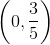All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : X And Y Intercept
What is the 

The 




The 

Example Question #124 : Grade 8
Give the 
The graph has no 
The graph has no 
The 




However, since this expression has 0 in a denominator, it is of undefined value. This means that there is no value of 


Example Question #2 : X And Y Intercept
Give the 
The graph has no 
The 




The 

Example Question #131 : Grade 8
Give the 

The graph does not have a 
The 




The 

Example Question #4 : How To Find X Or Y Intercept
A line passes through 


The line has no 
First, find the slope of the second line 

The equation is now in the slope-intercept form 


The first line, being perpendicular to the second, has as its slope the opposite of the reciprocal of 

Therefore, we are looking for a line through 

with

the equation becomes

To find the 


The 

Example Question #5 : How To Find X Or Y Intercept
A line passes through 


The line has no 
First, find the slope of the second line 

The equation is now in the slope-intercept form 


The first line, being parallel to the second, has the same slope.
Therefore, we are looking for a line through 

with

the equation becomes

To find the 


The 

Example Question #6 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6
Give the 


The line has no 
By the point-slope formula, this line has the equation
where
By substitution, the equation becomes

To find the 


The 

Example Question #6 : How To Find X Or Y Intercept
Give the 


The line has no 
First, find the slope of the line, using the slope formula
setting 
By the point-slope formula, this line has the equation
where

or
To find the 


The 

Example Question #132 : Grade 8
Give the 


First, find the slope of the line, using the slope formula
setting 
By the point-slope formula, this line has the equation
where

or
To find the 


The 

Example Question #7 : How To Find X Or Y Intercept
Give the 


By the point-slope formula, this line has the equation
where
By substitution, the equation becomes

To find the 


The 

Certified Tutor
All SSAT Upper Level Math Resources