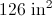We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Geometry

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 … 22 23 Next →

Example Question #3 : How To Find A Rectangle On A Coordinate Plane

Dr. Robinson recently put a rectangular fence around his backyard. The fence has a width of $\small 15$ yards and a length of $\small 8$ yards. If Dr. Robinson paid $\small \small \$ 12.50$ for every yard of fence, how much did the fence cost?

Possible Answers:

$\small \$625$

$\small \$575$

$\small \$525$

$\small \$375$

Correct answer:

$\small \$575$

Explanation:

To find the cost of the fence, apply the formula $\small P=2(width)+2(length)$ in order to first find the length of the perimeter of the fence.

Then multiply the perimeter by $\small \$12.50$ .

Thus, the solution is:

$\small P=2(15)+2(8)$
$\small P=30+16$
$\small P=46$

$\small 46\times12.5=575$

Report an Error

Example Question #4 : How To Find A Rectangle On A Coordinate Plane

Custom_vt_xy_gif_file_13abcd

The rectangle shown above has a width of $\small 14$ and a length of $\small 4$ . Find the area and perimeter of the rectangle.

Possible Answers:

$\small \small A=50 units^2, P=34$

$\small \small A=56 units^2, P=36$

$\small \small A=43 units^2, P=26$

$\small \small A=36 units^2, P=36$

Correct answer:

$\small \small A=56 units^2, P=36$

Explanation:

To solve this problem apply the formulas: $\small Area=width\times length$ & $\small Perimeter=2(w)+2(l)$

Thus, the solution is:

$\small A=14\times4=56$
$\small P=2(14)+2(4)=28+8=36$

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

A right triangle has legs 90 centimeters and 16 centimeters, What is its area?

Possible Answers:

$256 \; \textrm{cm}^{2}$

$405\; \textrm{cm}^{2}$

$720 \; \textrm{cm}^{2}$

$4,050 \; \textrm{cm}^{2}$

$1,440 \; \textrm{cm}^{2}$

Correct answer:

$720 \; \textrm{cm}^{2}$

Explanation:

The legs of a right triangle are its base and height, so use the area formula for a triangle with these dimension. Setting b=16,h=90 :

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 16 \cdot 90= 720$

Report an Error

Example Question #1 : Plane Geometry

A triangle has base 18 inches and height 14 inches. What is its area?

Possible Answers:

$98 \; \textrm{in}^{2}$

$162 \; \textrm{in}^{2}$

$196 \; \textrm{in}^{2}$

$252 \; \textrm{in}^{2}$

$126 \; \textrm{in}^{2}$

Correct answer:

$126 \; \textrm{in}^{2}$

Explanation:

Use the area formula for a triangle, setting b=18,h=14 :

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 18 \cdot14 = 126$

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

Triangle

What is the area of the above triangle?

Possible Answers:

$168\textrm{ in}^{2}$

$112\textrm{ in}^{2}$

$56\textrm{ in}^{2}$

$300\textrm{ in}^{2}$

$84\textrm{ in}^{2}$

Correct answer:

$84\textrm{ in}^{2}$

Explanation:

The two legs of a right triangle can serve as its base and its height. The area of the triangle is half the product of the two:

$\frac{1}{2} \cdot 7 \cdot 24 = 84$

That is, the area is 84 square inches.

Report an Error

Example Question #2 : How To Find The Area Of A Triangle

Triangle

What is the area of the above triangle?

Possible Answers:

$300\textrm{ mm}^{2}$

$6,000\textrm{ mm}^{2}$

$3,000\textrm{ mm}^{2}$

$325\textrm{ mm}^{2}$

$3,250\textrm{ mm}^{2}$

Correct answer:

$3,000\textrm{ mm}^{2}$

Explanation:

The two legs of a right triangle can serve as its base and its height. The area of the triangle is half the product of the two:

$\frac{1}{2} \cdot 50 \cdot 120 = 3,000$

That is, the area is 3,000 square millimeters.

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

Triangle

Note: Figure NOT drawn to scale.

The above triangle has an area of 450 square centimers. $x = 20 \textrm{ cm}$ . What is ?

Possible Answers:

$y = 30\textrm{ cm}$

$y = 60\textrm{ cm}$

$y = 45\textrm{ cm}$

$y = 22.5 \textrm{ cm}$

$y = 37.5\textrm{ cm}$

Correct answer:

$y = 45\textrm{ cm}$

Explanation:

The area of a triangle is one half the product of its base and its height - in the above diagram, that means

$A = \frac{1}{2}xy$ .

Substitute A = 450, x = 20 , and solve for :

$\frac{1}{2} \cdot 20 \cdot y = 450$

$10 \cdot y = 450$

$10 \cdot y \div 10 = 450 \div 10$

$y = 45 \textrm{ cm}$

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

Find the area of the triangle.

Note: Figure not drawn to scale.

Possible Answers:

$60\: in^{2}$

$120\: in^{2}$

$24\: in^{2}$

$48\: in^{2}$

Correct answer:

$60\: in^{2}$

Explanation:

To find the area of a triangle, multiply the base of the triangle by the height and then divide by two.

10*12=120

120/2=60

Report an Error

Example Question #7 : How To Find The Area Of A Triangle

Square

The quadrilateral in the above diagram is a square. What percent of it is white?

Possible Answers:

$28 \frac{1}{8} \%$

$20 \%$

$14 \frac{1}{16} \%$

$17 \frac{1}{2} \%$

$16 \frac{1}{4} \%$

Correct answer:

$14 \frac{1}{16} \%$

Explanation:

The area of the entire square is the square of the length of a side, or

$80 \times 80 = 6,400$ .

The area of the white right triangle is half the product of its legs, or

$\frac{1}{2} \times 30 \times 60 = 900$ .

Therefore, the area of that triangle is

$\frac{900 }{6,400} \times 100 = 14 \frac{1}{16} \%$

of that of the entire square.

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

Yard_2

Mr. Jones owns the isosceles-triangle-shaped parcel of land seen in the above diagram. He sells the parcel represented in red to his brother. What is the area of the land he retains?

Possible Answers:

$7,616\textrm{ m}^{2}$

$11,200\textrm{ m}^{2}$

$18,816\textrm{ m}^{2}$

$15,232\textrm{ m}^{2}$

$4,032\textrm{ m}^{2}$

Correct answer:

$7,616\textrm{ m}^{2}$

Explanation:

The area of a triangle is half the product of its base and its height, so Mr. Jones's parcel originally had area

$\frac{1}{2} \times 140 \times 160 = 11,200$ square meters.

The portion he sold his brother, represented by the red right triangle, has area

$\frac{1}{2} \times 56 \times 128 = 3,584$ square meters.

Therefore, the area of the parcel Mr. Jones retained is

11,200 -3,584= 7,616 square meters.

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 … 22 23 Next →

View SSAT- Middle Level Tutors

Daniel
Certified Tutor

Stony Brook University, Bachelors, Biology, General. SUNY College of Optometry, PHD, Optometry.

View SSAT- Middle Level Tutors

Justin
Certified Tutor

Boston College, Bachelor in Arts, Philosophy. Montclair State University, Master of Arts Teaching, Education.

View SSAT- Middle Level Tutors

Alexandra
Certified Tutor

University of Kent, Bachelor of Science, Mathematics.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Miami, SAT Tutors in Dallas Fort Worth, Computer Science Tutors in Seattle, French Tutors in Denver, French Tutors in Atlanta, Physics Tutors in Denver, ACT Tutors in Boston, GMAT Tutors in Los Angeles, ACT Tutors in Los Angeles, Physics Tutors in San Diego

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Miami, MCAT Courses & Classes in Boston, SAT Courses & Classes in New York City, GRE Courses & Classes in Phoenix, LSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Miami, ACT Test Prep in Miami, MCAT Test Prep in Boston, MCAT Test Prep in New York City, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Atlanta, LSAT Test Prep in Washington DC, MCAT Test Prep in Philadelphia, LSAT Test Prep in Miami, SAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Geometry

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #3 : How To Find A Rectangle On A Coordinate Plane

Example Question #4 : How To Find A Rectangle On A Coordinate Plane

Example Question #1 : How To Find The Area Of A Triangle

Example Question #1 : Plane Geometry

Example Question #1 : How To Find The Area Of A Triangle

Example Question #2 : How To Find The Area Of A Triangle

Example Question #1 : How To Find The Area Of A Triangle

Example Question #1 : How To Find The Area Of A Triangle

Example Question #7 : How To Find The Area Of A Triangle

Example Question #1 : How To Find The Area Of A Triangle

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: