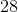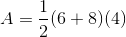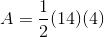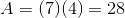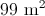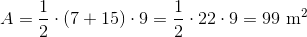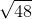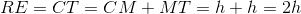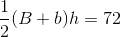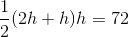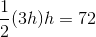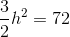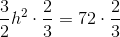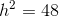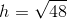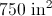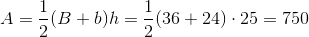Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Geometry

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

Find the area of the trapezoid:

Question_7

Possible Answers:

Correct answer:

Explanation:

The area of a trapezoid can be determined using the equation $A=\frac{1}{2}(b_1+b_2)h$ .

$A=\frac{1}{2}(6+8)(4)$

$A=\frac{1}{2}(14)(4)$

A=(7)(4)=28

Report an Error

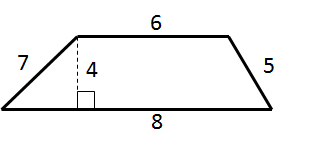
Example Question #1 : How To Find The Area Of A Trapezoid

Trapezoid

What is the area of the trapezoid?

Possible Answers:

$135\textrm{ m}^{2}$

$198\textrm{ m}^{2}$

$63\textrm{ m}^{2}$

$105\textrm{ m}^{2}$

$99\textrm{ m}^{2}$

Correct answer:

$99\textrm{ m}^{2}$

Explanation:

To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.

$A = \frac{1}{2} \cdot (7 + 15) \cdot 9 = \frac{1}{2} \cdot 22 \cdot 9 = 99 \textrm{ m}^2$

Report an Error

Example Question #392 : Ssat Middle Level Quantitative (Math)

Trapezoid

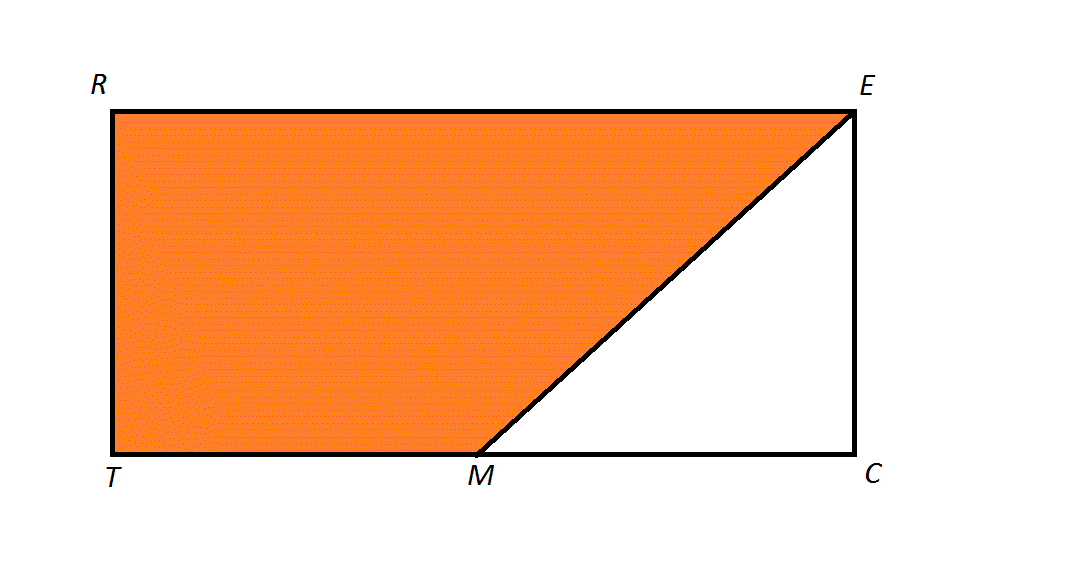
The above diagram depicts a rectangle RECT with isosceles triangle $\Delta ECM$ . If is the midpoint of $\overline{CT}$ , and the area of the orange region is , then what is the length of one leg of $\Delta ECM$ ?

Possible Answers:

$\sqrt {96}$

$\sqrt {48}$

$\sqrt {108}$

$\sqrt {54}$

Correct answer:

$\sqrt {48}$

Explanation:

The length of a leg of $\Delta ECM$ is equal to the height of the orange region, which is a trapezoid. Call this length/height .

Since the triangle is isosceles, then CM = h , and since is the midpoint of $\overline{CT}$ , MT = h . Also, since opposite sides of a rectangle are congruent,

RE = CT = CM + MT = h + h = 2h

Therefore, the orange region is a trapezoid with bases and and height . Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:

$\frac{1}{2} (B + b)h = 72$

$\frac{1}{2} (2h + h)h = 72$

$\frac{1}{2} (3h )h = 72$

$\frac{3}{2}h^{2} = 72$

$\frac{3}{2}h^{2} \cdot \frac{2}{3} = 72 \cdot \frac{2}{3}$

$h^{2}= 48$

$h = \sqrt {48}$

This is the length of one leg of the triangle.

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

A trapezoid has a height of inches and bases measuring inches and inches. What is its area?

Possible Answers:

$1,500\; \textrm{in}^{2}$

$750\; \textrm{in}^{2}$

$864\; \textrm{in}^{2}$

$900\; \textrm{in}^{2}$

$600\; \textrm{in}^{2}$

Correct answer:

$750\; \textrm{in}^{2}$

Explanation:

Use the following formula, with B = 36,b = 24,h=25 :

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (36+24) \cdot 25 = 750$

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

What is the area of a trapezoid with height 20 inches and bases of length 100 and 200?

Possible Answers:

$1,000\; \textrm{in}^{2}$

$3,000\; \textrm{in}^{2}$

$6,000\; \textrm{in}^{2}$

$2,000\; \textrm{in}^{2}$

$4,000\; \textrm{in}^{2}$

Correct answer:

$3,000\; \textrm{in}^{2}$

Explanation:

Set B=200 , b=100 , h = 20 .

The area of a trapezoid can be found using this formula:

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (200+100) \cdot 20 = 3,000$

The area is 3,000 square inches.

Report an Error

Example Question #1 : Lines

Lines

Figure NOT drawn to scale.

AE = 80, AB = x, BC = x + 4, CD = 2x+1, DE = x-6

Evaluate .

Possible Answers:

13.8

16.2

17.8

15.2

12.8

Correct answer:

16.2

Explanation:

By the Segment Addition Postulate,

AB + BC + CD + DE = AE

x + (x+4) + (2x+1) + (x-6) = 80

5x-1= 80

5x-1+1 = 80+1

5x = 81

$5x \div 5 = 81 \div 5$

x = 16.2

AB = x = 16.2

Report an Error

Example Question #1 : How To Find Length Of A Line

A right triangle has one leg with a length of 6 feet and a hypotenuse of 10 feet. What is the length of the other leg?

Possible Answers:

$8\ \text{ft}$

$6\ \text{ft}$

$5\ \text{ft}$

$10\ \text{ft}$

$4\ \text{ft}$

Correct answer:

$8\ \text{ft}$

Explanation:

In geometry, a right angle triangle can occur with the ratio of 3:4:5 in which 3 and 4 are each leg lengths, and 5 is the hypotenuse.

When you know the length of two sides of a right angle triangle like this, you can calculate the third side using this ratio.

Here, the ratio is:

6:x:10

This is double the 3:4:5 ratio. Therefore, we should multiply 4 by 2 in order to solve for the missing leg, which would be a value of 8 feet.

Another way to solve is to use the Pythagorean Theorem: a^2+b^2=c^2 .

We know that one leg is 6 feet and the hypotenuse is 10 feet.

(6)^2+b^2=(10)^2

36+b^2=100

b^2=64

$b=\sqrt{64}=8$

Report an Error

Example Question #2 : Lines

The radius of a circle is 6 inches. What is one-third of the diameter?

Possible Answers:

$2\ \textup{inches}$

$12\ \textup{inches}$

$4\ \textup{inches}$

$7\ \textup{inches}$

$6\ \textup{inches}$

Correct answer:

$4\ \textup{inches}$

Explanation:

If the radius is equal to 6 inches, then the diameter will be double that value, or 12 inches. One-third of 12 is 4, which is therefore the correct answer.

Report an Error

Example Question #3 : Lines

A right triangle has one leg with length $5\:cm$ and another leg with length $8\:cm$ . What is the length of the hypotenuse?

Possible Answers:

10.5

$\sqrt{55}$

$\sqrt{67}$

$\sqrt{89}$

Correct answer:

$\sqrt{89}$

Explanation:

Since we are dealing with a right triangle, we can use the Pythagorean Theorem:

$a^{2}+b^{2}=c^{2}$ ,

where and are leg lengths of and , respectively, and is the length of the hypotenuse.

Substituting values into the Theorem:

$5^{2}+8^{2}=c^{2}$

$25+64=c^{2}$

$89=c^{2}$

$\sqrt{89}=c$

Report an Error

Example Question #2 : Lines

Line has a length of $60\:cm$ . It is bisected at point , and the resulting segment is bisected again at point . What is the length of the line segment ?

Possible Answers:

$20\:cm$

$30\:cm$

$15\:cm$

$45\:cm$

$7.5\:cm$

Correct answer:

$15\:cm$

Explanation:

A line that is bisected is split into two segments of equal length. Therefore, if line is bisected at point ,

$AC=\frac{1}{2}AB=30\: cm$ .

Consequently, bisecting line segment at point :

$AD=\frac{1}{2}AC=\frac{1}{2}(30)=15\:cm$

Report an Error

View SSAT- Middle Level Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View SSAT- Middle Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View SSAT- Middle Level Tutors

Darron
Certified Tutor

Georgia State University, Bachelors, English Education . Liberty University, Masters, Education.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in San Francisco-Bay Area, Computer Science Tutors in Boston, GRE Tutors in Los Angeles, Math Tutors in Phoenix, ACT Tutors in Houston, MCAT Tutors in Washington DC, Calculus Tutors in Dallas Fort Worth, SAT Tutors in San Francisco-Bay Area, Calculus Tutors in Miami, Biology Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Phoenix, ISEE Courses & Classes in Washington DC, MCAT Courses & Classes in Seattle, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Phoenix, SAT Courses & Classes in Phoenix, SAT Courses & Classes in Denver

Popular Test Prep

SAT Test Prep in Los Angeles, SAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Chicago, LSAT Test Prep in Denver, MCAT Test Prep in San Diego, GMAT Test Prep in Miami, GRE Test Prep in Denver, MCAT Test Prep in Seattle, SAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Geometry

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #392 : Ssat Middle Level Quantitative (Math)

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #1 : Lines

Example Question #1 : How To Find Length Of A Line

Example Question #2 : Lines

Example Question #3 : Lines

Example Question #2 : Lines

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: