SSAT Middle Level Math : Geometry
Study concepts, example questions & explanations for SSAT Middle Level Math
All SSAT Middle Level Math Resources
Example Questions
Example Question #32 : How To Find The Area Of A Rectangle
What is the value of 
Given that there are 360 degrees in a quadrilateral,
Example Question #343 : Ssat Middle Level Quantitative (Math)
If the length of a rectangle is 7.5 feet and the width is 2 feet, what is the value of 
The area of a rectangle is calculated by multiplying the length by the width. Here, the length is 7.5 and the width is 2, so the area will be 15.
Given that the area is also equal to 
Example Question #81 : Quadrilaterals
If a cereal box has a volume of 40 cubic inches, a width of 2 inches, and a height of 5 inches, what is its length?
The formula for the volume of a rectangular solid is 
Use the provided information from the question in the above formula and solve for the length.
Therefore, the length of the box is 4 inches. In answering this question, it is important to look at the units before selecting an answer. It is easy to be tricked into thinking that because the total answer is in cubic inches that it may be necessary to have square inches, but when multiplying three values, each with inches as their units, the units of the product will be cubic inches.
Example Question #3 : How To Find The Volume Of A Figure
One cubic meter is equal to one thousand liters.
The above depicts a rectangular swimming pool for an apartment. The pool is 
The pool can be seen as a rectangular prism with dimensions 
One cubic meter is equal to one thousand liters, so multiply:
Example Question #345 : Ssat Middle Level Quantitative (Math)
Which of the following is equal to the area of a rectangle with length 
Multiply each dimension by 
Multiply these dimensions to get the area of the rectangle in square centimeters:
Example Question #81 : Quadrilaterals
The above depicts a rectangular swimming pool for an apartment. The pool is five feet deep everywhere.
An apartment manager wants to paint the four sides and the bottom of the swimming pool. One one-gallon can of the paint he wants to use covers 
The bottom of the swimming pool has area
There are two sides whose area is
and two sides whose area is
Add the areas:
One one-gallon can of paint covers 350 square feet, so divide:
Seven full gallons and part of another are required, so eight is the correct answer.
Example Question #84 : Quadrilaterals
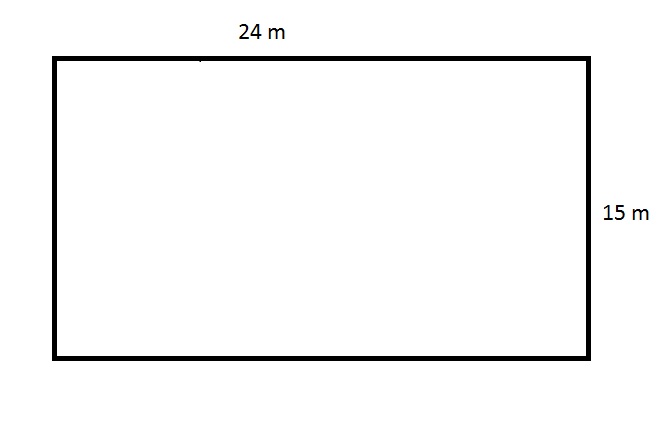
You are putting in a new carpet in your living room. The dimensions of the the room are 
To find the area of a rectangle, you must multiply the two different side lengths. For this room the answer would be 
Example Question #85 : Quadrilaterals
Refer to the above figures. The square at left has area 160. Give the area of the rectangle at right.
The area of the square, whose sides have length 
The square and the rectangle have the same area, so the correct response is 160.
Example Question #41 : How To Find The Area Of A Rectangle
Figure NOT drawn to scale.
Figure 1 and Figure 2 have the same area. The shaded portion of Figure 1 has area 64. What is the area of the shaded portion of Figure 2?
Figure 1 is a rectangle divided into 24 squares of equal size; 3 of the squares are shaded, which means that 
Figure 2 is a circle divided into 8 sectors of equal size; 1 is shaded, which means that 
Since the two figures are of the same area, the two shaded portions, each of which have an area that is the same fraction of this common area, must themselves have the same area. Since the shaded portion of Figure 1 has area 64, so does the shaded portion of Figure 2.
Example Question #1 : How To Find The Area Of A Parallelogram
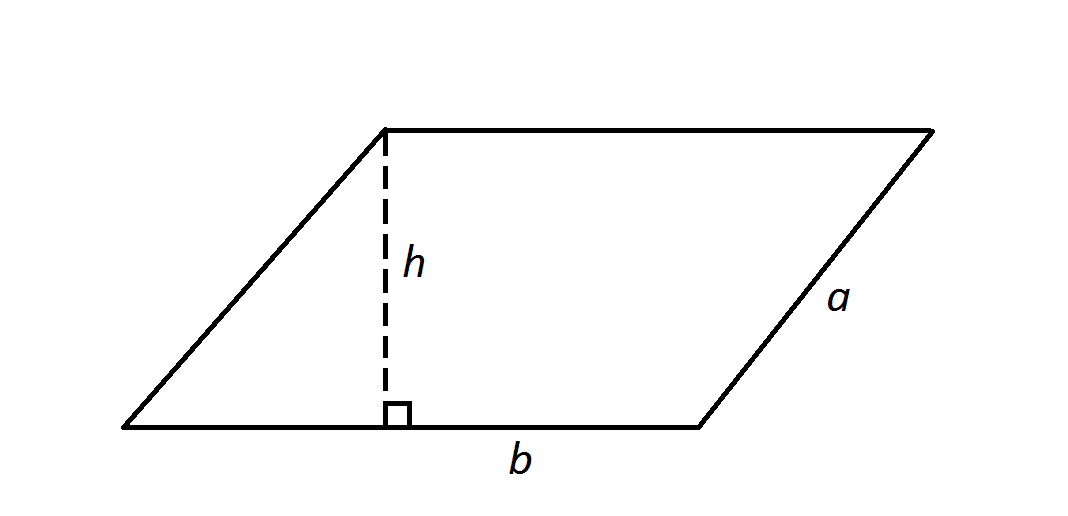
Note: Figure NOT drawn to scale
In the above diagram,
Give the area of the parallelogram.
The area of a parallelogram is its base multiplied by its height - represented by 
Note that the value of 
Certified Tutor
All SSAT Middle Level Math Resources
