All SSAT Middle Level Math Resources
Example Questions
Example Question #91 : Plane Geometry

The rectangle above is inches long and inches wide. What is the area of the rectangle?
Note: Figure not drawn to scale.
The area of the rectangle is . In order to find the area of a rectangle, multiply the length (5 inches) by the width (10 inches). The answer is in units2 because the area, by definition, is the number of square units that cover the inside of a figure.
Example Question #1 : How To Find The Volume Of A Figure
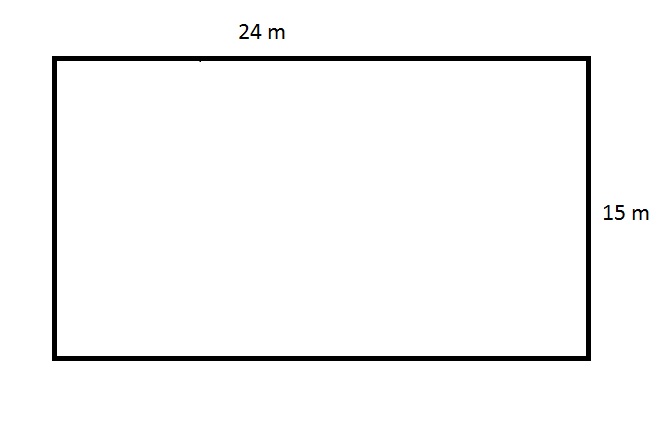
The above depicts a rectangular swimming pool for an apartment. The pool is two meters deep everywhere. What is the volume of the pool in cubic meters?
The correct answer is not among the other choices.
The pool can be seen as a rectangular prism with dimensions 24 meters by 15 meters by 2 meters; its volume is the product of these dimensions, or
cubic meters.
Example Question #4 : Geometry

Note: Figure NOT drawn to scale.
What percent of the above figure is white?
The large rectangle has length 80 and width 40, and, consequently, area
.
The white region is a rectangle with length 30 and width 20, and, consequently, area
.
The white region is
of the large rectangle.
Example Question #2 : How To Find The Area Of A Rectangle
What is the area of a rectangle with length and width ?
The formula for the area, , of a rectangle when we are given its length, , and width, , is .
To calculate this area, just multiply the two terms.
Example Question #11 : Geometry
Order the following from least area to greatest area:
Figure A: A rectangle with length 10 inches and width 14 inches.
Figure B: A square with side length 1 foot.
Figure C: A triangle with base 16 inches and height 20 inches.
Figure A has area square inches.
Figure B has area square inches, 1 foot being equal to 12 inches.
Figure C has area square inches.
The figures, arranged from least area to greatest, are A, B, C.
Example Question #2 : How To Find The Area Of A Rectangle

Give the surface area of the above box in square inches.
Use the surface area formula, substituting :
square inches
Example Question #1 : Area
The area of a rectangle can be found by multiplying the length by the width.
Example Question #61 : Quadrilaterals

Give the area of the above rectangle in square feet.
Since 1 yard = 3 feet, multiply each dimension by 3 to convert from yards to feet:
Use the area formula, substituting :
square feet
Example Question #92 : Plane Geometry
The ratio of the perimeter of one square to that of another square is . What is the ratio of the area of the first square to that of the second square?
For the sake of simplicity, we will assume that the second square has sidelength 1; Then its perimeter is , and its area is .
The perimeter of the first square is , and its sidelength is . The area of this square is therefore .
The ratio of the areas is therefore .
Example Question #31 : Rectangles
The following question is about the Jones family wanting to buy square foot tiles for their rectangular basement. Their basement perimeter is 74 feet, with one of the sides being 15 feet long.
How many square foot titles are the Jones family needing to purchase in order to tile their basement?
From the given information we know that the perimeter of the rectangular basement is 74 feet. We also know that one side of the rectangular basement is 15 feet. This means that the opposite side is also 15 feet long because the equivalent opposite sides rule of rectangles. In order to find the lengths of our other two sides of the rectangle, we need to subtract our two 15 feet sides from the perimeters 74 feet.
.
We know that the last two sides have to add up to 44 feet. Since the rules of rectangles say opposite sides are equivalent, we must take 44 feet and divide by the 2 sides. So 44 divided by 2 is 22 feet, meaning each side must be 22 feet. After adding up all the sides we can confirm that our perimeter is 74 feet.
Now we know all the sides of the rectangle, we are able to move to the next step, finding the area. We must find the area, because the tiles are square feet. So in order to find the area we must take the length of the rectangle and multiply it to the width.
Knowing the area of the rectangular basement we also know how many tile are needed to fill the basement for the Jones family. It is exactly 330 square feet tile needed.
Certified Tutor
All SSAT Middle Level Math Resources


































































































