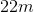SSAT Elementary Level Math : SSAT Elementary Level Quantitative (Math)
Study concepts, example questions & explanations for SSAT Elementary Level Math
All SSAT Elementary Level Math Resources
Example Questions
Example Question #581 : Geometry
Use the following rectangle to answer the question:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, let's look at the rectangle.
We can see the length is 6in. Because it is a rectangle, the opposite side is also 6in.
We can also see the width of the rectangle is 3in. Because it is a rectangle, the opposite side is also 3in.
Knowing this, we can substitute into the formula. We get
Example Question #581 : Plane Geometry
Use the following rectangle to solve the problem:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, given the rectangle
we can see the length is 11in. Because it is a rectangle, the opposite side is also 11in.
The width is 5in. Because it is a rectangle, the opposite side is also 5in.
So, we can substitute.
Example Question #582 : Geometry
What is the width of the rectangle if the perimeter is 
The formula for perimeter of a rectangle is
To solve for the width we can plug our known values into the equation.
Subtract 
Divide 
Example Question #81 : Apply Area And Perimeter Formulas For Rectangles: Ccss.Math.Content.4.Md.A.3
What is the length of a room with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #5741 : Ssat Elementary Level Quantitative (Math)
Emily is digging a garden in her backyard that is 
The formula for perimeter of a rectangle is
To solve for the perimeter we can plug our known values into the equation.
Example Question #71 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Example Question #201 : Quadrilaterals
David wants to put a fence around a garden in his backyard. How much fencing will he need if his garden is 
The fence is going around the backyard, so this is a perimeter problem.
Example Question #581 : Plane Geometry
The altitude of a triangle is given as 
The area of a triangle is given by 
altitude
base 
Therefore:
Area
Example Question #1 : Triangles
What is the area of a triangle with a base of 11 and a height of 4?
6
60
22
14
44
22
The formula to find the area of a triangle is 
Example Question #2 : How To Find The Area Of A Triangle
You can find the area of a triangle if you know ___________.
the perimeter
its angles
two side lengths
the height and base
the height and base
All SSAT Elementary Level Math Resources
