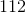Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Elementary Level Math : SSAT Elementary Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Elementary Level Math

Create An Account

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find The Area Of A Triangle

Squareslice

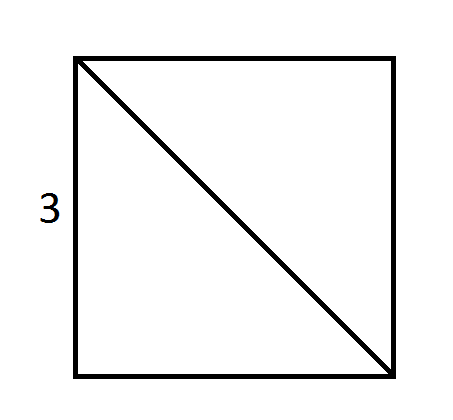
The square shown above has a side length of 3 and is divided into two triangles by its diagonal. What is the area of one of the triangles?

Possible Answers:

12.25

4.5

6.5

Correct answer:

4.5

Explanation:

The area of the square is side times side, $3\times3=9$ .

Each triangle is half of the square, $9\div2=4.5$ .

Report an Error

Example Question #4 : How To Find The Area Of A Triangle

Screen_shot_2014-01-10_at_1.07.49_pm

What is the area of the triangle?

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a triangle is

$\frac{base \times height}{2}$

First, we should multiply (base) $\times$ (height), to get a total of .

Next, we need to divide by , which gives us a total area of .

Report an Error

Example Question #2 : How To Find The Area Of A Triangle

An isosceles triangle has a base of 12 cm and a height of 6 cm. What is the area of the triangle?

Possible Answers:

$36\: cm^{2}$

$72\: cm^{2}$

$12\: cm^{2}$

$18\, cm^{2}$

Correct answer:

$36\: cm^{2}$

Explanation:

To find the area of a triangle, you must multiply $\frac{1}{2}$ by the base (12 cm) by the height (6 cm):

$\frac{12\: cm}{2}\times6 \: cm=36\: cm^{2}$

Therefore the area of this triangle is $36\: cm^{2}$ .

Report an Error

Example Question #1 : Triangles

A triangle has a base of 14 and a height of 8. What is the area of the triangle?

Possible Answers:

112

Correct answer:

Explanation:

To find the area of a triangle, multiply the base (14) by the height (8) and divide by 2:

$\frac{14}{2}\times8=56$

Therefore the area of this triangle is .

Report an Error

Example Question #4 : How To Find The Area Of A Triangle

Screen_shot_2014-01-06_at_12.34.19_pm

What is the area of the triangle?

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a triangle is $\frac{base \times height}{2}$ .

$A = \frac{6\times 8}{2}=24$

Report an Error

Example Question #1 : How To Find The Area Of A Triangle

If a triangle has a base of 3 inches and a height of 8 inches, what is the area of the triangle?

Possible Answers:

$11\;in^2$

$24\;in^2$

$32\;in^2$

$16\;in^2$

$12\;in^{2}$

Correct answer:

$12\;in^{2}$

Explanation:

The formula for the area of a triangle is $\frac{1}{2} \times base \times height= area$ .

Plug in the values given to solve the equation:

$\frac{1}{2}(3\;in)(8\;in)=$

$\frac{1}{2}\times 3\;in \times 8\;in = \frac{1}{2}\;\times24\;in^{2}=12\;in^2$

Report an Error

Example Question #2 : How To Find The Area Of A Triangle

A triangle has a base of 10 centimeters and a height of 12 centimeters. What is the area of the triangle?

Possible Answers:

$70\ cm^{2}$

$120\ cm^{2}$

$60\ cm^{2}$

$72\ cm^{2}$

$22\ cm^{2}$

Correct answer:

$60\ cm^{2}$

Explanation:

The formula for the area of a triangle is $area=\frac{1}{2}(base)(height)$ .

Plug in the given values to solve for the area:

$\frac{1}{2}\times10cm\times12cm$

= $5cm\times12cm$

= 60cm^2

The area of this triangle is $60cm^{2}$ .

Report an Error

Example Question #591 : Geometry

What is the area of a right triangle with a base of length 4 and a height that is 3 times longer than the base?

Possible Answers:

Correct answer:

Explanation:

The area of a triangle is given by the formula $A = \frac{1}{2}\times b \times h$ , where is the length of the base and is the height.

First let's figure out the height. The base is 4, and the height is 3 times greater than the base:

$3 \times 4 = 12$

Now plug the base and height into the area formula:

$A = 0.5 \times 4 \times 12 = 2 \times 12 = 24$

The area of the triangle is 24.

Report an Error

Example Question #601 : Plane Geometry

A triangle has base of length units and a height of length units. What is the area of this triangle?

Possible Answers:

units squared

Correct answer:

units squared

Explanation:

To calculate the area of a triangle, you use the formula $\frac{1}{2}\cdot b\cdot h$ , where is the length of the base of the triangle and is the height of the triangle. For this triangle, we need to solve the equation $\frac{1}{2}\cdot 6 \cdot 8$ to find its area. $6\cdot 8=48$ and $48\div2=24$ , so the triangle's area is units squared.

Report an Error

Example Question #11 : Triangles

The base of a triangle is , and the height is . What is the area of the triangle?

Possible Answers:

180

240

120

Correct answer:

120

Explanation:

Write the formula for area of a triangle. Substitute the dimensions.

$A=\frac{bh}{2} = \frac{(12)(20)}{2} = 12(10)=120$

Report an Error

View SSAT- Elementary Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

View SSAT- Elementary Level Tutors

Jeneen
Certified Tutor

College of Charleston, Bachelor of Science, Elementary School Teaching.

View SSAT- Elementary Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Phoenix, Math Tutors in Atlanta, Statistics Tutors in Philadelphia, English Tutors in Philadelphia, Algebra Tutors in Chicago, MCAT Tutors in San Francisco-Bay Area, ACT Tutors in Denver, Reading Tutors in Philadelphia, GMAT Tutors in New York City, GMAT Tutors in Dallas Fort Worth

Popular Courses & Classes

GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Boston, Spanish Courses & Classes in Boston, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in Denver, SSAT Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles

Popular Test Prep

SAT Test Prep in Chicago, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, MCAT Test Prep in San Diego, ACT Test Prep in Los Angeles, GMAT Test Prep in Washington DC, MCAT Test Prep in Boston, ISEE Test Prep in Los Angeles, SAT Test Prep in San Diego, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Elementary Level Math : SSAT Elementary Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Elementary Level Math

All SSAT Elementary Level Math Resources

Example Questions

Example Question #3 : How To Find The Area Of A Triangle

Example Question #4 : How To Find The Area Of A Triangle

Example Question #2 : How To Find The Area Of A Triangle

Example Question #1 : Triangles

Example Question #4 : How To Find The Area Of A Triangle

Example Question #1 : How To Find The Area Of A Triangle

Example Question #2 : How To Find The Area Of A Triangle

Example Question #591 : Geometry

Example Question #601 : Plane Geometry

Example Question #11 : Triangles

All SSAT Elementary Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: