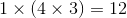All SSAT Elementary Level Math Resources
Example Questions
Example Question #21 : Apply Properties Of Operations As Strategies To Multiply And Divide: Ccss.Math.Content.3.Oa.B.5
Select the answer that demonstrates the associative property of multiplication for






The associative property of multiplication says that we can group numbers in any order to multiply them and our product, or answer, will be the same.

Example Question #572 : Common Core Math: Grade 3
Select the answer that demonstrates the associative property of multiplication for






The associative property of multiplication says that we can group numbers in any order to multiply them and our product, or answer, will be the same.

Example Question #573 : Common Core Math: Grade 3
Select the answer that demonstrates the associative property of multiplication for






The associative property of multiplication says that we can group numbers in any order to multiply them and our product, or answer, will be the same.

Example Question #574 : Common Core Math: Grade 3
Select the answer that demonstrates the associative property of multiplication for






The associative property of multiplication says that we can group numbers in any order to multiply them and our product, or answer, will be the same.

Example Question #3071 : Ssat Elementary Level Quantitative (Math)
Fill in the missing piece of the table.

To solve this problem we can set up a proportion and cross multiply to solve for our unknown.
First we cross multiply.

Then we divide each side by 

Example Question #3072 : Ssat Elementary Level Quantitative (Math)
Fill in the missing piece of the table.

To solve this problem we can set up a proportion and cross multiply to solve for our unknown.
First we cross multiply.

Then we divide each side by 

Example Question #3073 : Ssat Elementary Level Quantitative (Math)
Which sequence below follows the rule of multiplying
The only sequence that multiplies 
Example Question #3074 : Ssat Elementary Level Quantitative (Math)
Which sequence below follows the rule of multiplying
The only sequence that multiplies 
Example Question #3075 : Ssat Elementary Level Quantitative (Math)
What is the pattern for the numbers in the X column to the numbers in the Y column?

Multiply
Add
Add
Multiply
Subtract
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #791 : Operations & Algebraic Thinking
What is the pattern for the numbers in the X column to the numbers in the Y column?

Subtract
Add
Add
Multiply
Divide
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Certified Tutor
Certified Tutor
All SSAT Elementary Level Math Resources