All SAT Math Resources
Example Questions
Example Question #1 : Spheres
A cube with volume 27 cubic inches is inscribed inside a sphere such that each vertex of the cube touches the sphere. What is the radius, in inches, of the sphere?
√3/2 (approximately 1.73)
8.5
9
(3√3)/2 (approximately 2.60)
(3√3)/2 (approximately 2.60)
We know that the cube has a volume of 27 cubic inches, so each side of the cube must be ∛27=3 inches. Since the cube is inscribed inside the sphere, the diameter of the sphere is the diagonal length of the cube, so the radius of the sphere is half of the diagonal length of the cube. To find the diagonal length of the cube, we use the distance formula d=√(32+32+32 )=√(3*32 )=3√3, and then divide the result by 2 to find the radius of the sphere, (3√3)/2.
Example Question #1 : Spheres
The surface area of a sphere is 100π square feet. What is the radius in feet?
5
π
10
100
25
5
S = 4π(r2)
100π = 4π(r2)
100 = 4r2
25 = r2
5 = r
Example Question #771 : Sat Mathematics
What is the radius of a sphere with a surface area of 16?
In order to find the radius, first write the surface area formula for a sphere and substitute the surface area.
Divide by 

Simplify both sides of the equation.
Square root both sides.
The radius is 
Example Question #781 : Sat Mathematics
Find the diameter of a sphere with a surface area of 
Write the formula to find the surface area of a sphere.
Substitute the area and solve for the radius.
The diameter is double the radius.
Example Question #782 : Sat Mathematics
What is the diameter of a sphere if the surface area is 
Write the formula for the surface area of a sphere.
Substitute the area and find the radius.
The diameter is double the radius.
Example Question #6 : Spheres
What is the diameter of a sphere with a volume of 
Write the formula for the volume of a sphere.
Substitute the volume.
Multiply by 

Cube root both sides.
The diameter is double the radius.
The answer is:
Example Question #242 : Geometry
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
256π
32π
128π
16π
64π
16π
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
Example Question #12 : How To Find Surface Area
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
1/2
3/4
1
2/3
3/2
3/4
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4πr2, where r is the length of the radius.
Each hemisphere will have the following shape:
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = πr2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4πr2.
area of curved part of hemisphere = (1/2)4πr2 = 2πr2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = πr2 + 2πr2 = 3πr2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3πr2)/(4πr2) = 3/4
The answer is 3/4.
Example Question #1 : Spheres
The volume of a sphere is 2304π in3. What is the surface area of this sphere in square inches?
36π
216π
576π
144π
None of the other answers
576π
To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:
V = (4/3)πr3
For our data, we can say:
2304π = (4/3)πr3; 2304 = (4/3)r3; 6912 = 4r3; 1728 = r3; 12 * 12 * 12 = r3; r = 12
Now, based on this, we can ascertain the surface area using the equation:
A = 4πr2
For our data, this is:
A = 4π*122 = 576π
Example Question #1 : Spheres
A sphere has its center at the origin. A point on its surface is found on the x-y axis at (6,8). In square units, what is the surface area of this sphere?
(400/3)π
400π
40π
200π
None of the other answers
400π
To find the surface area, we must first find the radius. Based on our description, this passes from (0,0) to (6,8). This can be found using the distance formula:
62 + 82 = r2; r2 = 36 + 64; r2 = 100; r = 10
It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).
The rest is easy. The surface area of the sphere is defined by:
A = 4πr2 = 4 * 100 * π = 400π
All SAT Math Resources






















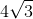


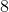





![2\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573825/gif.latex)
![2\sqrt[3]{\frac{18}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573826/gif.latex)
![\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573829/gif.latex)
![\sqrt[3]{\frac{18}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573827/gif.latex)





![\sqrt[3]{\frac{9}{\pi}}= r](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574190/gif.latex)
![d= 2\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574191/gif.latex)
![2\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574192/gif.latex)



