All SAT Math Resources
Example Questions
Example Question #244 : New Sat
Mrs. Smith's 8th grade class has a weekly quiz. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. Examining the graph, what type of correlation if any, exists?

The graph depicts a positive correlation.
The graph depicts a negative correlation.
The graph depicts a constant correlation.
The graph depicts no correlation.
More information is needed.
The graph depicts a negative correlation.
Mrs. Smith's 8th grade class had a quiz last week. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. In other words, the graph in this particular question is a dot plot and the question asks to find a correlation if one exists.
Recall that a correlation is a trend seen in the data. Graphically, trends can be either:
I. Positive
II. Negative
III. Constant
IV. No trend
For a trend to be positive the x and y variable both increase. A trend is negative when the y variable (dependent variable) decreases as the x variable (independent variable) increases. A constant trend occurs when the y variable stays the same as the x variable increases. No trend exists when the data appears to be scattered with no association between the x and y variables.

Examining the graph given it is seen that the x variable is the number of questions missed and the y variable is the overall score on the quiz. It is seen that as the number of questions missed increases, the overall score on the quiz decreases. This describes a negative trend.
In other words, the graph depicts a negative correlation.
Example Question #271 : Coordinate Geometry
Given the graph of record sales, what fraction of records were sold in 2004 to 2010?

Given the graph of record sales, to find the fraction of records that were sold in 2004 to 2010 first identify the record sales in 2004 and the record sales in 2010.
Examining the graph,
Record sales in 2004:14 million
Record sales in 2010: 13 million
From here, to find the fraction of records sold during this time period, use the following formula.
Example Question #661 : Sat Mathematics
Which of the following coordinate pairs is farthest from the origin?
Using the distance formula, calculate the distance from each of these points to the origin, (0, 0). While each answer choice has coordinates that add up to seven, (-1, 8) is the coordinate pair that produces the largest distance, namely 
Example Question #272 : Coordinate Geometry
On the coordinate plane, the point with coordinates 
Quadrant IV
Quadrant I
None of these
Quadrant III
Quadrant II
Quadrant II
On the coordinate plane, a point with a negative 
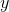
Example Question #662 : Sat Mathematics
A line graphed on the coordinate plane below. 
Give the equation of the line in slope intercept form.
The slope of the line is 

The equation of the line is 
Example Question #2 : Graphing

Give the equation of the curve.
None of the other answers
 This is the parent graph of
This is the parent graph of 

Example Question #666 : Sat Mathematics
Give the area of the triangle on the coordinate plane that is bounded by the lines of the equations 


It is necessary to find the coordinates of the vertices of the triangle, each of which is the intersection of two of the three lines.
The intersection of the lines of the equations 





The intersection of the lines of the equations 




This point of intersection is 
The intersection of the lines of the equations 




Since 


The lines in question are graphed below, and the triangle they bound is shaded:

We can take the horizontal side as the base of the triangle; its length is the difference of the 
The height is the vertical distance from this side to the opposite side, which is the difference of the 
The area is half their product:
Example Question #1 : Geometry
Billy set up a ramp for his toy cars. He did this by taking a wooden plank and putting one end on top of a brick that was 3 inches high. He then put the other end on top of a box that was 9 inches high. The bricks were 18 inches apart. What is the slope of the plank?
The value of the slope (m) is rise over run, and can be calculated with the formula below:
The coordinates of the first end of the plank would be (0,3), given that this is the starting point of the plank (so x would be 0), and y would be 3 since the brick is 3 inches tall.
The coordinates of the second end of the plank would be (18,9) since the plank is 18 inches long (so x would be 18) and y would be 9 since the box was 9 inches tall at the other end.
From this information we know that we can assign the following coordinates for the equation:

Below is the solution we would get from plugging this information into the equation for slope:
This reduces to
Example Question #663 : Sat Mathematics
What is the slope of the line depicted by the graph?

Looking at the graph, it is seen that the line passes through the points (-8,-5) and (8,5).

The slope of a line through the points 


in the slope formula:
Example Question #661 : Geometry

What is the 
This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a linear function.
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general algebraic function for the given graph.
Since the graph is that of a straight line, the general algebraic form of the function is,
where
Step 2: Identify where the graph crosses the 

Therefore the general form of the function looks like,
Step 3: Answer the question.
The 
Certified Tutor
Certified Tutor
All SAT Math Resources