All SAT Math Resources
Example Questions
Example Question #1 : Lines

Refer to the above diagram. The plane containing the above figure can be called Plane 
False
True
False
A plane can be named after any three points on the plane that are not on the same line. As seen below, points 



Therefore, Plane 
Example Question #691 : Geometry

Refer to the above figure.
True or false: 

False
True
True
Two rays are opposite rays, by definition, if
(1) they have the same endpoint, and
(2) their union is a line.
The first letter in the name of a ray refers to its endpoint; the second refers to the name of any other point on the ray. 









The union of the two rays is a line. Both criteria are met, so the rays are indeed opposite.
Example Question #1541 : Plane Geometry

Refer to the above diagram:
True or false: 

False
True
False
A line can be named after any two points it passes through. The line 

The line does not pass through 


Example Question #1583 : Basic Geometry

Refer to the above diagram.
True or false: 

True
False
False
By definition, two angles comprise a pair of vertical angles if
(1) they have the same vertex; and
(2) the union of the two angles is exactly a pair of intersecting lines.
In the figure below, 


While the two angles have the same vertex, their union is not a pair of intersecting lines. The two angles are not a vertical pair.
Example Question #1585 : Basic Geometry

Refer to the above diagram.
True or false: 

True
False
False
By definition, two angles form a linear pair if and only if
(1) they have the same vertex;
(2) they share a side; and,
(3) their interiors have no points in common.
In the figure below, 


The two angles have the same vertex and share no interior points. However, they do not share a side. Therefore, they do not comprise a linear pair.
Example Question #1 : Solid Geometry

The above image is a silo made from two right circular cones, and a right circular cylinder where the dimensions are given in feet. Of the following answers, which one best represents the volume of the entire silo in cubic feet?
To solve this, we need to break it down into three parts.
Example Question #1 : How To Find The Length Of An Edge Of A Cube
The number of square units in the surface area of a cube is twice as large as the number of cubic units in its volume. What is the cube's volume, in cubic units?
108
9
36
216
27
27
The number of square units in the surface area of a cube is given by the formula 6s2, where s is the length of the side of the cube in units. Moreover, the number of cubic units in a cube's volume is equal to s3.
Since the number of square units in the surface area is twice as large as the cubic units of the volume, we can write the following equation to solve for s:
6s2 = 2s3
Subtract 6s2 from both sides.
2s3 – 6s2 = 0
Factor out 2s2 from both terms.
2s2(s – 3) = 0
We must set each factor equal to zero.
2s2 = 0, only if s = 0; however, no cube has a side length of zero, so s can't be zero.
Set the other factor, s – 3, equal to zero.
s – 3 = 0
Add three to both sides.
s = 3
This means that the side length of the cube is 3 units. The volume, which we previously stated was equal to s3, must then be 33, or 27 cubic units.
The answer is 27.
Example Question #1 : Solid Geometry
You own a Rubik's cube with a volume of . What is the edge length of the cube?
No enough information to solve.
You own a Rubik's cube with a volume of . What is the edge length of the cube?
To solve for edge length, think of the volume of a cube formula:
Now, we have the volume, so just rearrange it to solve for side length:
Example Question #1 : Solid Geometry
If a cube is 3” on all sides, what is the length of the diagonal of the cube?
27
3√2
3√3
9
4√3
3√3
General formula for the diagonal of a cube if each side of the cube = s
Use Pythagorean Theorem to get the diagonal across the base:
s2 + s2 = h2
And again use Pythagorean Theorem to get cube’s diagonal, then solve for d:
h2 + s2 = d2
s2 + s2 + s2 = d2
3 * s2 = d2
d = √ (3 * s2) = s √3
So, if s = 3 then the answer is 3√3
Example Question #2 : Solid Geometry
A cube is inscribed in a sphere of radius 1 such that all 8 vertices of the cube are on the surface of the sphere. What is the length of the diagonal of the cube?
√(3)
√(2)
8
2
1
2
Since the diagonal of the cube is a line segment that goes through the center of the cube (and also the circumscribed sphere), it is clear that the diagonal of the cube is also the diameter of the sphere. Since the radius = 1, the diameter = 2.
All SAT Math Resources









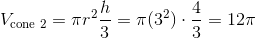






![s=\sqrt[3]{343cm^3}=7cm](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/809640/gif.latex)



