All SAT Math Resources
Example Questions
Example Question #3 : Hexagons

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?
One mile is equal to 5,280 feet; one fourth of a mile is equal to

Each of the six congruent sides measures one sixth of this, or
Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of

Example Question #2 : Hexagons
190
180
200
170
210
Example Question #1 : Hexagons
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by 

Example Question #21 : Plane Geometry
Find the sum of all the inner angles in a hexagon.
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
Example Question #21 : Geometry
An equilateral triangle with side length 
Because it can be split into two 
With that in mind, the equilateral triangle in question has area of 
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is 
Example Question #1 : How To Find The Area Of A Hexagon
Calculate the approximate area a regular hexagon with the following side length:
Cannot be determined
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the given problem we know that the side length of a regular hexagon is the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Round the answer to the nearest whole number.
Example Question #1 : Triangles
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
18
87
3
7
90
87
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
Example Question #2 : Triangles
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
45
30
90
65
60
30
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
Example Question #1021 : High School Math
In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?
50
10
20
30
40
10
In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.
Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.
x + y + 90 = 180
Subtract 90 from both sides.
x + y = 90
Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:
y – 10 + 2x – 20 + 90 = 180
y + 2x + 60 = 180
Subtract 60 from both sides.
y + 2x = 120
We have a system of equations consisting of x + y = 90 and y + 2x = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.
x + y = 90
Subtract x from both sides.
y = 90 – x
Next, we can substitute 90 – x into the equation y + 2x = 120.
(90 – x) + 2x = 120
90 + x = 120
x = 120 – 90 = 30
x = 30
Since y = 90 – x, y = 90 – 30 = 60.
The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2x – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.
The answer is 10.
Example Question #191 : Triangles
Which of the following sets of line-segment lengths can form a triangle?
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
All SAT Math Resources









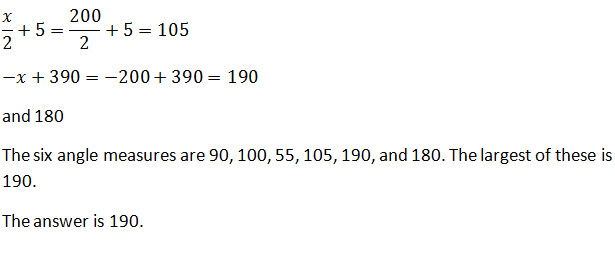


















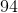













![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)

















