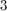First, we need to find all of the factors of 48. One way to do this is to come up with all of the pairs of positive integers that will multiply to yield 48. The pairs are as follows:

1 * 48

2 * 24

3 * 16

4 * 12

6 * 8

This means that the facors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. Note that there are ten factors. 

The question asks us for the percentage of the factors of 48 that are also factors of 168. This means we must see which of the ten factors 48 are also factors of 48. One way to do this is do divide 168 by each of the factors of 48 and see which give us whole numbers. If we divide 168 by a factor of 48 and get a whole number, then this number is also a factor of 168. 

168/1 = 168

168/2 = 84

168/3 = 56

168/4 = 42

168/6 = 28

168/8 = 21

168/12 = 14

168/16 = 10.5

168/24 = 7

168/48 = 3.5

So, when we divided 168 by the factors of 48, we obtained a whole number, except when we divided by 16 and 48. This means that 16 and 48 are not factors of 168; however, 1, 2, 3, 4, 6, 8, 12, and 24 are all factors of 168.

Thus, out of the ten factors of 48, there are eight which are also factors of 168. We must express 8 out of 10 as a percent. 8/10 = 0.80 = 80%.

The answer is 80.

Only 7 hole spaces can fit. 8 * 6 = 48, which would be 2 feet longer than the wall.

Let's look at each statement separately and see if it must be true.

First, let's consider 0 # (k + m) = 0.

This statement essentially says that if we divide 0 by the sum of k and m, the remainder should be 0. In general, when 0 is divided by an integer (other than itself), the result is zero with a remainder of zero. For example, if 0 is divided by 2, then 2 will go into zero exactly zero times with a remainder of zero. Because the sum of k and m is an integer, this means that zero divided by (k + m) will also have a remainder of zero. Thus, 0 # (k + m) = 0 is true.

Next, let's examine m # m = 0. This statement says that if we divide m by itself, we should get a remainder of zero. This is true, because any integer divided by itself is equal to 1, with a remainder of zero. Remember that the result of using the # symbol only gives us the remainder. Therefore m # m = 0, not 1. 

Let's now look at k # k = m # m.

As we established previously, m # m = 0. Similarly, k # k = 0, because any integer divided by itself produces a remainder of zero. Because m # m and k # k both equal zero, they are also equal to each other. Thus, k # k = m # m is indeed true.

Next, let's consider (k²) # k = 0. This says that if we square an integer and then divide the result by the integer, we should get a remainder of zero. This is true, because an integer is always a factor of its square. In other words, the square of an integer is always divisible by the integer. And if one number is divisible by another, then the resulting quotient has a remainder of zero. For example (5²) # 5 = 0, because when we divide 25 by 5, we get 5 with a remainder of zero. Again, remember that we are only concerned with the remainder. 

By the process of elmination, the answer is (km) # k = m. Let's see why this statement must be false. The product of k and m has factors k and m. For example, the product of 4 and 3, which equals 12, has the factors 4 and 3. When a number is divided by one of its factor, the resulting remainder must be zero. For example (4(3)) # 4 = 12 # 4 = 0, because the remainder when 12 is divided by 4 is equal to zero. Thus (km) # k = 0, not m. 

The answer is (km) # k = m.

We will essentially have to represent 180 as a product of prime factors, because 2, 3, 5, and 7 are all prime numbers. The easiest way to do this will be to find the prime factorization of 180.

180 = 18(10)= (9)(2)(10) = (3)(3)(2)(10)=(3)(3)(2)(2)(5) = . Because 7 is not a factor of 180, we can mutiply the prime factorization of 180 by (which equals 1) in order to get 7 into our prime factorization.

 =

In order for to equal , the exponents of each base must match. This means that a = 2, b = 2, c = 1, and d = 0. The sum of a, b, c, and d is 5.

The answer is 5.

The prime factorization of 24 is (2)(2)(2)(3).  The distinct primes are 2 and 3, the product of which is 6.

Since 7 is prime, its only prime factor is itself.

Multiples of 12 are found by multiplying 12 by a whole number.  Some examples include:

Clearly, the smallest positive value obtainable is 12.  Do not confuse the term multiple with the term factor!

Begin by identifying the prime factors of 210. This can be done easily using a factoring tree (see image).

 The prime factors of 210 are 2, 3, 5 and 7. Of these factors, three of them are greater than 2. 

The smallest multiple of 9 within the given range is .

The largest multiple of 9 within the given range is .

Counting the numbers from 6 to 11, inclusive, yields 6.

 is the only choice that is both a multiple of  and a perfect square.