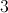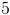The word "product" refers to the answer of a multiplication problem.  Since 2 times 8 equals 16, it is a valid pair of numbers.

If  is an odd integer then we can plug 1 into  and solve for  yielding 13. 13 is prime, meaning it is only divisible by 1 and itself.

Recall that when you multiply by an even number, you get an even product.

Therefore, we know the following from the first statement:

 is even or  is even or both  and  are even.

For the second, we know this:

Since  is even, therefore,  can be either even or odd. (Regardless of what it is, we can get an even value for .)  

Based on all this data, we can tell nothing necessarily about . If  is even, then  is even, even if  is odd. However, if  is odd while  is even, then  will be even.

In a group of philosophers,  are followers of Durandus. Twice that number are followers of Ockham. Four times the number of followers of Ockham are followers of Aquinas. One sixth of the number of followers of Aquinas are followers of Scotus. How many total philosophers are in the group?

To start, let's calculate the total philosophers:

Ockham:  * <Number following Durandus>, or 

Aquinas:  * <Number following Ockham>, or 

Scotus:  divided by , or 

Therefore, the total number is:

I is not always true because a negative number multiplied by 7 will give a number that is more negative than the original. II is true because adding 5 to any number will increase the value. III is true because squaring any number will increase the magnitude of the value, and squaring a negative number will make it positive.

There are certain patterns that can be used to predict whether the product or sum of numbers will be odd or even. The sum of two odd numbers is always even, as is the sum of two even numbers. The sum of an odd number and an even number is always odd. In multiplication the product of two odd numbers is always odd. While the product of even numbers, as well as the product of odd numbers multiplied by even numbers is always even. So for this problem we need to find scenarios where the only possibile answers are even.  can only result in even numbers no matter what positive integers are used for  and , because  must can only result in even products; the same can be said for . The rules provide that the sum of two even numbers is even, so  is the answer.

By choosing a random negative number, for example: –4, we can input the number into each choice and see if we come out with another negative number.  When we put –4 in for x, we would have –4 – (–(–4)) or –4 – 4, which is –8.  Plugging in the other options gives a positive answer.  You can try other negative numbers, if needed, to confirm this still works. 

x: –7 – 7= –7 + –7 = –14

y: –7 – (–7) = –7 + 7 = 0

when subtracting a negative number, turn it into an addition problem

Reconvert  into single signs.  Remember that double negatives will turn into a positive.

Subtracting a negative number moves the number farther left of the zero digit on the number line. 

The answer is: