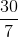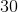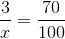All SAT Math Resources
Example Questions
Example Question #41 : Percentage
17 is 85% of what number?
In this case, 17 is part of a whole x. We are also given that 17 is 85% of x.
With this in mind, we can set up the following proportion.
To solve for x, cross multiply.
Example Question #21 : Whole And Part
On the ride home from school, Jim notices that 

Let x represent the total number of cars Jim sees on the way home. If Jim sees 7 yellow cars and notices that 35% of all the cars he sees are yellow, then we can express this as
7/x = 35%, or
Using cross multiplication, we see that
Therefore, Jim sees 20 total cars on the way home. The question wants to know how many cars are NOT yellow. We can find that by subtracting the total number of cars from the number of yellow cars:
Example Question #22 : Whole And Part


None of the given answers are correct.
To solve this problem, we can set up a proportion and solve for our missing value using cross multiplication.
Example Question #23 : Whole And Part


Don't let the pi throw you off on this question. We can set up a proportion to solve for the whole that we are looking for.
(Remember that any percentage can also be written as a fraction.)
Now we can solve for our unknown by using cross multiplication.
Therefore, 


Example Question #44 : Percentage


We can set up a proportion to solve this problem. Remember that we can express percentages as fractions.
Now we can cross-multiply and solve for our unknown.
Example Question #2011 : Psat Mathematics
55 and 1/2% of 23 is about what?
155
13
11
49
2
13
55 and 1/2% can be written as a decimal: 0.555. To see what number is about 55.5% of 23, multiply 0.555 by 23. Answer: 12.765 or about 13.
Another route is to say that 55.5% is about half of 23. Half of 23 is 11.5. Since 55.5% is greater than 50%, 13 is the logical choice instead of 11.
Example Question #2012 : Psat Mathematics
Let x and y be numbers such that x and y are both nonzero, and x > y. If half of x is equal to thirty percent of the positive difference between x and y, then what is the ratio of x to y?
–3/2
–1
3/2
2/3
–2/3
–3/2
We need to find expressions for fifty percent of x and for thirty percent of the positive difference between x and y. Then, we can set these two expressions equal to each other and determine the ratio of x to y.
Fifty percent of x is equal to one-half of x, which is the same as multiplying x by 0.50.
50% of x = 0.5x
Thirty percent of the positive difference between x and y means that we need to multiply the positive difference between x and y by thirty percent. Because x > y, the positive difference between x and y is equal to x – y. We then need to take thirty percent of the quantity x – y. Remember that to convert from a percent to a decimal, we move the decimal two spaces to the left. Therefore, 30% = 0.30. We can now multiply this by (x – y).
30% of x – y = 0.30(x – y)
Now, we set the two expressions equal to one another.
0.5x = 0.30(x – y)
Distribute the right side.
0.5x = 0.3x – 0.3y
The ratio of x to y is represent by x/y. Thus, we want to group the x and y terms on opposite sides of the equations, and then divide both sides by y.
0.5x = 0.3x – 0.3y
Subtract 0.3x from both sides.
0.2x = –0.3y
Divide both sides by 0.2
x = (–0.3/0.2)y
Divide both sides by y to find x/y.
x/y = (–0.3/0.2) = –1.5.
Because the answers are in fractions, we want to rewrite –1.5 as a fraction. We can write –1.5 as –1.5/1 and then mutiply the top and bottom by 2.
(–1.5/1)(2/2) = –3/2
The answer is –3/2
Example Question #1091 : Sat Mathematics
If 









133
125
25
100
75
75
We are told that 50% of x is equal to 25% of y. We need to represent these two pieces of information as algebraic expressions. We can convert 50% and 25% to decimals by moving the decimals two places to the left. Thus, 50% = 0.50, and 25% = 0.25. To find 50% of x, we multiply x by 0.50. In other words, 50% of x = 0.50x. Likewise, 25% of y = 0.25y. We now set 0.50x and 0.25y equal to one another.
0.50x = 0.25y
Let's divide both sides by 0.25 to get rid of decimals.
2x = y
Next, we are told that 40% of y is equal to 60% of z. We will represent 40% and 60% as 0.40 and 0.60, respectively. Thus, we can write the following equation:
0.40y = 0.60z
Ultimately, we are asked to find x as a percentage of z. This means we want to find an equation with x and z, but not y. If we solve for y in the second equation, and then substitute this value into the first, we can eliminate y.
Let's take the equation 0.40y = 0.60z and divide both sides by 0.40.
y = 1.5z
Now, we can take 1.5z and substitute this for y in the first equation.
2x = 1.5z
In order to find x as a percent of z, we must solve for x in terms of z. This means we must divide both sides of the equation by 2.
x = 0.75z
x is 0.75 times z. We can represent 0.75 as 75%, because in order to convert from a decimal to a percent, we need to move the decimal two spaces to the right. Therefore, if x = 0.75z, then x = 75% of z.
The answer is 75.
Example Question #1 : Decimals And Percentage
What is 
The correct answer is 
This can be obtained by taking the percentage of 

This shifts the decimal place over two places to the left, which results in 

Example Question #2 : How To Find Decimal Equivalent To A Percentage
Find the decimal equivalent to the percentage:
In order to find the decimal equivalent of a percentage, the number that makes up the percent has to be divided by 100. However, since it is division by a power of 10, we can accomplish the same thing, by moving the decimal point 2 places to the left, thus making the number smaller. For this problem, that looks like this:
Certified Tutor
All SAT Math Resources