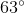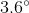All SAT Math Resources
Example Questions
Example Question #233 : Sat Mathematics
A square has an area of 
The area of the given square is given by 

Example Question #232 : Sat Mathematics
Find the perimeter of a square with side length 4.
To solve, simply use the formula for the perimeter of a square.
Substitute in the side length of four into the following equation.
Thus,
Example Question #231 : Geometry
Find the perimeter of a square whose side length is 5.
To solve, simply use the formula for the perimeter of a square. Thus,
Example Question #233 : Sat Mathematics
Find the perimeter of a square with side length 12.
To solve, simply use the formula for the perimeter of the square. Thus,
If you don't remember the formula, you can simply sum the sides of a square to find the perimeter.
However, since all the sides area the same, we get the following.
Example Question #231 : Plane Geometry
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
2
1
4
16
2
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
Example Question #621 : Geometry
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
18
14
15
17
16
15
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Example Question #241 : Geometry
If the area of a square is 25 inches squared, what is the perimeter?
20
10
15
25
Not enough information
20
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

Example Question #261 : Plane Geometry
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
II and III only
II only
I and II only
I only
I, II, and III
I only
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
Example Question #187 : New Sat
If a polygon has 10 sides, what is the measure of each exterior angle?
In order to figure this out, we need to remember the formula for finding exterior angles. 
So the measure of each exterior angle is 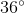
Example Question #1 : Quadrilaterals
A rhombus has a side length of 5. Which of the following is NOT a possible value for its area?
30
10
15
24
25
30
The area of a rhombus will vary as the angles made by its sides change. The "flatter" the rhombus is (with two very small angles and two very large angles, say 2, 178, 2, and 178 degrees), the smaller the area is. There is, of course, a lower bound of zero for the area, but the area can get arbitrarily small. This implies that the correct answer would be the largest choice. In fact, the largest area of a rhombus occurs when all four angles are equal, i.e. when the rhombus is a square. The area of a square of side length 5 is 25, so any value bigger than 25 is impossible to acheive.
All SAT Math Resources