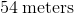Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Quadrilaterals

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Rectangle

A rectangle is x inches long and 3x inches wide. If the area of the rectangle is 108, what is the value of x?

Possible Answers:

Correct answer:

Explanation:

Solve for x

Area of a rectangle A = lw = x(3x) = 3x² = 108

x² = 36

x = 6

Report an Error

Example Question #4 : Rectangles

If the area of rectangle is 52 meters squared and the perimeter of the same rectangle is 34 meters. What is the length of the larger side of the rectangle if the sides are integers?

Possible Answers:

16 meters

14 meters

13 meters

15 meters

12 meters

Correct answer:

13 meters

Explanation:

Area of a rectangle is = lw

Perimeter = 2(l+w)

We are given 34 = 2(l+w) or 17 = (l+w)

possible combinations of l + w

are 1+16, 2+15, 3+14, 4+13... ect

We are also given the area of the rectangle is 52 meters squared.

Do any of the above combinations when multiplied together= 52 meters squared? yes 4x13 = 52

Therefore the longest side of the rectangle is 13 meters

Report an Error

Example Question #33 : Quadrilaterals

Rectangles a

Figure is not drawn to scale.

The provided figure is a rectangle divided into two smaller rectangles, with

Rectangle $ABEF \sim$ Rectangle CDEB .

Which expression is equal to the length of $\overline{FE}$ ?

Possible Answers:

$12+ 2 \sqrt{5}$

$12 + 4\sqrt{5}$

$12+\sqrt{5}$

Correct answer:

$12 + 4\sqrt{5}$

Explanation:

Since Rectangle ABEF is similar to Rectangle CDEB , it follows that corresponding sides are in proportion. Specifically,

$\frac{FE}{BE} = \frac{BE}{DE}$

FE + DE = FD ;

since FD = 24 , if we let t = FE , then

t+ DE = 24 ,

and

DE= 24 - t

Setting BE = 8 , FE = t , and DE= 24 - t , the proportion statement becomes

$\frac{t}{8} = \frac{8}{24-t }$

Cross-multiplying, we get

$t(24-t) = 8 \cdot 8$

Simplifying, we get

$24t-t ^{2}= 64$

Since this is quadratic, all terms must be moved to one side:

$24t-t ^{2} - 24t + t ^{2} = 64 - 24t + t ^{2}$

$0= 64 - 24t + t ^{2}$

$t ^{2} - 24t + 64 = 0$

The solutions to quadratic equation

$ax^{2} + bx + c = 0$

can be found by way of the quadratic formula

$x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}$

Set a = 1, b= -24, c= 64 :

$x = \frac{-(-24) \pm \sqrt{(-24)^{2}-4(1)(64)}}{2(1)}$

$= \frac{ 24 \pm \sqrt{576-256}}{2}$

$= \frac{ 24 \pm \sqrt{320}}{2}$

Simplifying the radical using the Product of Radicals Property, we get

$\frac{ 24 \pm \sqrt{64}\cdot \sqrt{5}}{2}$

$=\frac{ 24 \pm8\sqrt{5}}{2}$

Splitting the fraction and reducing:

$\frac{ 24 }{2} \pm \frac{ 8\sqrt{5}}{2}$

$=12 \pm 4\sqrt{5}$

This actually tells us that the lengths of the two segments $\overline{FE}$ and $\overline{ED}$ have the lengths $12 + 4\sqrt{5}$ and $12 -4\sqrt{5}$ . $\overline{FE}$ is seen in the diagram to be the longer, so we choose the greater value, $12 + 4\sqrt{5}$ .

Report an Error

Example Question #1 : Rectangles

A rectangle has a width of 2x. If the length is five more than 150% of the width, what is the perimeter of the rectangle?

Possible Answers:

10(x + 1)

6x² + 5

5x + 10

6x² + 10x

5x + 5

Correct answer:

10(x + 1)

Explanation:

Given that w = 2x and l = 1.5w + 5, a substitution will show that l = 1.5(2x) + 5 = 3x + 5.

P = 2w + 2l = 2(2x) + 2(3x + 5) = 4x + 6x + 10 = 10x + 10 = 10(x + 1)

Report an Error

Example Question #1 : How To Find The Perimeter Of A Rectangle

Find the perimeter of a rectangle with width 7 and length 9.

Possible Answers:

$\frac{63}{2}$

Correct answer:

Explanation:

To solve, simply use the formula for the perimeter of a rectangle.

Substitute in the width of seven and the length of nine.

Thus,

P=2(w+l)=2*(7+9)=2*16=32

Report an Error

Example Question #2 : How To Find The Perimeter Of A Rectangle

Find the perimeter of a rectangle whose side lengths are 1 and 2.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the perimeter of a rectangle. Thus,

P=2(w+l)=2*(1+2)=2*3=6

Report an Error

Example Question #2 : How To Find The Perimeter Of A Rectangle

Find the perimeter of a rectangle with width 6 and length 9.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the perimeter.

P=2(w+l)

P=2*(6+9)=2*15=30

Another way to solve this problem is to add up all of the sides. Remember that even though only two values are given, a rectangle has 4 sides. Thus,

P=6+6+9+9=30

Report an Error

Example Question #1 : How To Find The Perimeter Of A Rectangle

You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?

Possible Answers:

4.5ft^2

12ft

9.5ft

9ft

Correct answer:

9ft

Explanation:

You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?

Perimeter of a rectangle is found via:

P=2l+2w=2(3ft)+2(1.5ft)=6ft+3ft=9ft

Report an Error

Example Question #3 : How To Find The Perimeter Of A Rectangle

Three of the vertices of a rectangle on the coordinate plane are located at the origin, (10, 0) , and (0, 7) . Give the perimeter of the rectangle.

Possible Answers:

Correct answer:

Explanation:

The rectangle in question is below:

Rectangle 3

The lengths of the rectangle is 10, the distance from the origin to (10,0) ; its width is 7, the distance from the origin to (0, 7) . The perimeter of a rectangle is equal to twice the sum of its length and width, so calculate:

$P= 2 (10+ 7 ) = 2 \times 17 = 34$ .

Report an Error

Example Question #8 : How To Find The Perimeter Of A Figure

A rectangular garden has an area of $80\: \mbox{m^2}$ . Its length is meters longer than its width. How much fencing is needed to enclose the garden?

Possible Answers:

$18\: \mbox{meters}$

$24\: \mbox{meters}$

$40\: \mbox{meters}$

$54\: \mbox{meters}$

$36\: \mbox{meters}$

Correct answer:

$36\: \mbox{meters}$

Explanation:

We define the variables as $w = \mbox{width}$ and $l = \mbox{length} = w + 2$ .

We substitute these values into the equation for the area of a rectangle and get $A_{\mbox{rectangle} }= wl = w(w + 2) = 80$ .

w^2 +2w-80=0

(w - 8)(w + 10) = 0

w = 8 or w = -10

Lengths cannot be negative, so the only correct answer is w = 8 . If w = 8 , then l = 10 .

Therefore, $\mbox{perimeter }= 2w + 2l = 16 + 20 = 36\:\mbox{m}$ .

Report an Error

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Mathematics Tutors

Miriam
Certified Tutor

Washington University in St Louis, Bachelor in Arts, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Denver, ISEE Courses & Classes in Chicago, GMAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Atlanta, Spanish Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver, Spanish Courses & Classes in New York City, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in New York City, SSAT Test Prep in Boston, GRE Test Prep in Denver, MCAT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Atlanta, SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Seattle, SSAT Test Prep in Washington DC, GMAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Quadrilaterals

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Rectangle

Example Question #4 : Rectangles

Example Question #33 : Quadrilaterals

Example Question #1 : Rectangles

Example Question #1 : How To Find The Perimeter Of A Rectangle

Example Question #2 : How To Find The Perimeter Of A Rectangle

Example Question #2 : How To Find The Perimeter Of A Rectangle

Example Question #1 : How To Find The Perimeter Of A Rectangle

Example Question #3 : How To Find The Perimeter Of A Rectangle

Example Question #8 : How To Find The Perimeter Of A Figure

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: