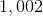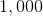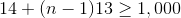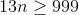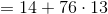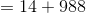Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Sequences

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Nth Term Of An Arithmetic Sequence

Consider the following sequence of numbers:

2, 9, 16, 23, ...

What will be the 8^th term in the sequence?

Possible Answers:

Correct answer:

Explanation:

Each number in the sequence in 7 more than the number preceding it.

The equation for the terms in an arithmetic sequence is a_n = a₁ + d(n-1), where d is the difference.

The formula for the terms in this sequence is therefore a_n = 2 + 7(n-1).

Plug in 8 for n to find the 8^th term:

a₈ = 2 + 7(8-1) = 51

Report an Error

Example Question #7 : How To Find The Nth Term Of An Arithmetic Sequence

Find the seventh term in the following sequence:

3,17,31,45,...

Possible Answers:

115

101

Correct answer:

Explanation:

The difference between each term can be found through subtraction. For example the difference between the first and the second term can be found as follows:

17-3=14

One can check and see that this is the case for the other given numbers in the sequence as well.

In order to find the seventh term, expand the sequence by adding 14 to the last given number (4th number) and all of the following numbers until the 7th number in the sequence is reached.

This gives the sequence:

3,17,31,45,59,73,87

As seen above the seventh number in the sequence is 87 and the correct answer.

Report an Error

Example Question #7 : Nth Term Of An Arithmetic Sequence

What is the tenth number in the sequence:

4, 7, 12, 19...

Possible Answers:

102

103

Correct answer:

103

Explanation:

The purpose of this question is to understand the patterns of sequences.

First, an equation for the $N^{th}$ term in the sequence must be determined ( $N^{2}+3$ ).

This is true because

N=1 will create 1^2+3=4 ,

N=2 will create 2^2+3=7 ,

N=3 will create 3^2+3=12 ,

N=4 will create 4^2+3=19 .

Then, the eqution must be applied to find the specified term. For the tenth term, the expression $10^{2}+3$ must be evaluated, yielding 103.

Report an Error

Example Question #4 : Nth Term Of An Arithmetic Sequence

You are given a sequence with the same difference between consecutive terms. We know it starts at and its 3rd term is . Find its 10th term.

Possible Answers:

Correct answer:

Explanation:

From the given information, we know -1+2x=5 , which means each consecutive difference is 3.

-1+9x=-1+9(3)=26

Report an Error

Example Question #7 : Nth Term Of An Arithmetic Sequence

An arithmetic sequence begins as follows:

12.8, 17.2, 21.6 , ...

Give the sixteenth term of this sequence.

Possible Answers:

None of the other responses give the correct answer.

70.0

83.2

78.8

74.4

Correct answer:

78.8

Explanation:

Subtract the first term $a_{1}$ from the second term $a_{2}$ to get the common difference :

$d = a_{2} - a_{1}$

Setting $a_{1} = 12 .8$ and $a_{2} = 17.2$

d = 17.2 - 12.8 = 4.4

The th term of an arithmetic sequence $a_{n}$ can be found by way of the formula

$a_{n} = a_{1}+ (n-1) d$

Setting n = 16 , $a_{1} = 12 .8$ , and d = 4.4 in the formula:

$a_{16} = 12.8 + (16-1) 4.4$

$= 12.8 + 15 \cdot 4.4$

= 12.8 +66

=78.8

Report an Error

Example Question #21 : Arithmetic Sequences

An arithmetic sequence begins as follows: 14, 27, 40...

What is the first four-digit integer in the sequence?

Possible Answers:

1,002

1,008

1,000

1,006

1,004

Correct answer:

1,002

Explanation:

Given the first two terms $a_{1}$ and $a_{2}$ , the common difference is equal to the difference:

$d = a_{2} - a_{1}$

Setting $a_{1} = 14$ , $a_{2} =27$ :

d = 27 - 14 = 13

The th term of an arithmetic sequence $a_{n}$ can be found by way of the formula

$a_{n} = a_{1}+ (n-1) d$

Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:

$a_{1}+ (n-1) d \ge 1,000$

Setting $a_{1} = 14$ and d = 13 and solving for :

$14 + (n-1) 13 \ge 1,000$

$14 + 13n-13 \ge 1,000$

$13n+1 \ge 1,000$

$13n+1 - 1 \ge 1,000 - 1$

$13 n \ge 999$

$13 n \div 13 \ge 999 \div 13$

$n \ge 76\frac{11}{13}$

Therefore, the 77th term, or $a_{77}$ , is the first element in the sequence greater than 1,000. Substituting n = 77 , $a_{1} = 14$ , and d = 13 in the rule and evaluating:

$a_{77}=a_{1}+ (n-1) d$

= 14+ (77-1) 13

$= 14+76 \cdot 13$

= 14+988

=1,002 ,

the correct choice.

Report an Error

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

$\small 2, 3, 5, 9, 17, x, 65, 129....$

$\small \textup{In the above number sequence, what is the value of}\,x?$

Possible Answers:

$\small 34$

$\small 35$

$\small 33$

$\small 31$

$\small 32$

Correct answer:

$\small 33$

Explanation:

Each term in the sequence is one less than twice the previous term.

So, $\small x=2\left ( 17\right )-1$

$\small x=33$

Report an Error

Example Question #2 : How To Find The Next Term In An Arithmetic Sequence

What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?

Possible Answers:

Correct answer:

Explanation:

The series is defined by n² – 1 starting at n = 1. The sixth number in the series then equal to 6² – 1 = 35.

Report an Error

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

A sequence of numbers is as follows:

3, 8, 18, 38, 78, . . .

What is the sum of the first seven numbers in the sequence?

Possible Answers:

248

490

1529

719

621

Correct answer:

621

Explanation:

The pattern of the sequence is (x+1) * 2.

We have the first 5 terms, so we need terms 6 and 7:

(78+1) * 2 = 158

(158+1) * 2 = 318

3 + 8 + 18 +38 + 78 + 158 + 318 = 621

Report an Error

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

Find the next term of the following sequence:

267, 256, 245, 234, 223,...

Possible Answers:

212

213

More information is needed

210

211

Correct answer:

212

Explanation:

The sequence provided is arithmetic. An arithmetic sequence has a common difference between each consecutive term. In this case, the difference is ; therefore, the next term is 212 .

You can also use a formula to find the next term of an arithmetic sequence:

$a_{n}=a_{n-1}+d$

where the current term and d = the common difference.

Report an Error

View SAT Mathematics Tutors

Aaqib
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Neuroscience.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Zachary
Certified Tutor

Yale University, Bachelor of Science, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Denver, ISEE Courses & Classes in Atlanta, ACT Courses & Classes in Houston, ACT Courses & Classes in Boston, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Miami, GRE Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Boston, ISEE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

GMAT Test Prep in Boston, MCAT Test Prep in Atlanta, ACT Test Prep in Chicago, GRE Test Prep in Philadelphia, MCAT Test Prep in Boston, GMAT Test Prep in Denver, SAT Test Prep in Chicago, ISEE Test Prep in Philadelphia, MCAT Test Prep in Miami, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Sequences

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : Nth Term Of An Arithmetic Sequence

Example Question #7 : How To Find The Nth Term Of An Arithmetic Sequence

Example Question #7 : Nth Term Of An Arithmetic Sequence

Example Question #4 : Nth Term Of An Arithmetic Sequence

Example Question #7 : Nth Term Of An Arithmetic Sequence

Example Question #21 : Arithmetic Sequences

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

Example Question #2 : How To Find The Next Term In An Arithmetic Sequence

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: