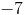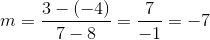We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : How to find slope of a line

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Other Lines

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

Possible Answers:

$\dpi{100} \small 3$

$\dpi{100} \small \frac{1}{5}$

$\dpi{100} \small 2$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small 5$

Correct answer:

$\dpi{100} \small 5$

Explanation:

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

Report an Error

Example Question #11 : How To Find Slope Of A Line

What is the slope of the line represented by the equation $6y-16x=7$ ?

Possible Answers:

$16$

$-16$

$\frac{8}{3}$

$6$

$\frac{7}{6}$

Correct answer:

$\frac{8}{3}$

Explanation:

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Report an Error

Example Question #222 : Geometry

What is the slope of the given linear equation?

2x + 4y = -7

Possible Answers:

-2

1/2

-1/2

-7/2

Correct answer:

-1/2

Explanation:

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Report an Error

Example Question #231 : Geometry

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Possible Answers:

$-\frac{1}{28}$

$\frac{1}{28}$

Correct answer:

Explanation:

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Report an Error

Example Question #12 : How To Find Slope Of A Line

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Possible Answers:

$4$

$-\frac{2}{3}$

$\frac{1}{2}$

$\frac{2}{3}$

$-\frac{1}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Report an Error

Example Question #13 : How To Find Slope Of A Line

What is the slope of a line running through points (7,3) and (8,-4) ?

Possible Answers:

$\frac{7}{3}$

$-\frac{1}{7}$

Correct answer:

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Report an Error

Example Question #508 : Geometry

Solve each problem and decide which is the best of the choices given.

Find the slope of the line for the given equation.
12x+3y=-6

Possible Answers:

$\frac{1}{4}$

$-\frac{1}{2}$

Correct answer:

Explanation:

For this problem, you have to solve for . We want to get the equation in slope-intercept form,

y=mx+b where represents the slope of the line.

12x+3y=-6

First subtract 12x from each side to get

3y=-12x-6 .

Then divide both sides by to get

y=-4x-2 .

The slope is the number in front of , so the slope is .

Report an Error

Example Question #504 : Geometry

Point is at (-2,-5) and point is at (3,1) . What is the slope of the line that connects the two points?

Possible Answers:

$\frac{6}{5}$

$-\frac{2}{3}$

$\frac{3}{2}$

$\frac{1}{5}$

$-\frac{6}{5}$

Correct answer:

$\frac{6}{5}$

Explanation:

The purpose of this question is to understand how the slope of a line is calculated.

The slope is the rise over the run, meaning the change in the y values over the change in the x values

$\frac{y_2-y_1}{x_2-x_1}$ .

So, the difference in y values divided by the difference in x values yields

$\frac{1-(-5)}{3-(-2)}=\frac{6}{5}$ .

Report an Error

Example Question #510 : Geometry

The following two points are located on the same line. What is the slope of the line?

$(2\pi, 5\pi), (11\pi, 6\pi)$

Possible Answers:

$9\pi$

$\frac{1}{9}$

$\frac{1}{9}\pi$

Correct answer:

$\frac{1}{9}$

Explanation:

The slope of a line with two points (x_1, y_1) and (x_2, y_2) is given by the following equation:

$m = \frac{y_2-y_1}{x_2-x_1}$

Let $(x_1, y_1) = (2\pi, 5\pi)$ and $(x_2, y_2) = (11\pi, 6\pi)$ . Substituting these values into the equation gives us:

$m = \frac{6\pi - 5\pi}{11\pi - 2\pi} = \frac{\pi}{9\pi} = \frac{1}{9}$

Report an Error

Example Question #15 : How To Find Slope Of A Line

Axes

Figure NOT drawn to scale

On the coordinate axes shown above, the shaded triangle has area 16.

Give the slope of the line that includes the hypotenuse of the triangle.

Possible Answers:

$-\frac{1}{2}$

None of the other choices gives the correct response.

$-\frac{1}{4}$

Correct answer:

Explanation:

The length of the horizontal leg of the triangle is the distance from the origin (0,0) to (4,0) , which is 4.

The area of a right triangle is half the product of the lengths of its legs and , so, setting a = 4 and A = 16 and solving for :

$\frac{1}{2} ab = A$

$\frac{1}{2} \cdot 4 \cdot b = 16$

2b = 16

$\frac{2b }{2}= \frac{16}{2}$

b = 8

Since this is the vertical distance from the origin, this is also the absolute value of the -coordinate of the -intercept of the line; also, this point is along the positive -axis. The line has -intercept (0,8) .

The slope of a line, given the intercepts (a,0) , (0, b) , is

$m = - \frac{b}{a}$ ,

Substitute a = 4 and b = 8 :

$m = - \frac{8}{4} = -2$ .

Report an Error

View SAT Mathematics Tutors

Momeena
Certified Tutor

State University of New York at New Paltz, Bachelors, Mathematics & Elementary Education. State University of New York at New...

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View SAT Mathematics Tutors

Scott
Certified Tutor

Rutgers College, Bachelors, Political Science and Government. Florida Coastal School of Law, PHD, Law.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Seattle, GMAT Courses & Classes in Phoenix, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Seattle, SSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Houston, GRE Courses & Classes in New York City, ISEE Courses & Classes in Boston, Spanish Courses & Classes in San Diego, GRE Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Seattle, ACT Test Prep in Miami, GMAT Test Prep in San Diego, SSAT Test Prep in Los Angeles, GRE Test Prep in Phoenix, SAT Test Prep in Boston, SSAT Test Prep in Atlanta, MCAT Test Prep in San Diego, SSAT Test Prep in San Diego, ACT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : How to find slope of a line

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : Other Lines

Example Question #11 : How To Find Slope Of A Line

Example Question #222 : Geometry

Example Question #231 : Geometry

Example Question #12 : How To Find Slope Of A Line

Example Question #13 : How To Find Slope Of A Line

Example Question #508 : Geometry

Example Question #504 : Geometry

Example Question #510 : Geometry

Example Question #15 : How To Find Slope Of A Line

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: