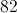Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : How to find absolute value

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Absolute Value

Define $p(x) = \frac{\left |x+2 \right |-1}{\left |x+1 \right |-2}$ .

Evaluate $p \left (-1 \frac{1}{5} \right )$ .

Possible Answers:

$-\frac{1} {9}$

$-\frac{1}{11}$

$\frac{1} {9}$

$\frac{1}{11}$

Correct answer:

$\frac{1} {9}$

Explanation:

$p(x) = \frac{\left |x+2 \right |-1}{\left |x+1 \right |-2}$ , or, equivalently,

$p(x) =\left ( \left |x+2 \right |-1 \right ) \div \left ( \left |x+1 \right |-2 \right )$

$p\left (-1 \frac{1}{5} \right )=\left ( \left |-1 \frac{1}{5}+2 \right |-1 \right ) \div \left ( \left |-1 \frac{1}{5}+1 \right |-2 \right )$

$=\left ( \left | \frac{4}{5} \right |-1 \right ) \div \left ( \left |- \frac{1}{5} \right |-2 \right )$

$=\left ( \frac{4}{5} -1 \right ) \div \left ( \frac{1}{5} -2 \right )$

$= - \frac{1}{5} \div \left ( - \frac{9}{5} \right )$

$= \frac{1}{5} \div \frac{9}{5}$

$= \frac{1}{5} \times \frac{5}{9}$

$= \frac{1} {9}$

Report an Error

Example Question #1 : How To Find Absolute Value

Define an operation $\triangleright$ as follows:

For all real numbers a,b ,

$a \triangleright b = \left | a- \frac{1}{2}b\right | + \left | \frac{1}{2} a+b\right |$

Evaluate $\frac{1}{3} \triangleright 4$ .

Possible Answers:

$6\frac{1}{2}$

$2\frac{1}{2}$

$\text{None of the other responses are correct.}$

$1\frac{1}{2}$

$5 \frac{5}{6}$

Correct answer:

$5 \frac{5}{6}$

Explanation:

$a \triangleright b = \left | a- \frac{1}{2}b\right | + \left | \frac{1}{2} a+b\right |$

$\frac{1}{3} \triangleright 4 = \left | \frac{1}{3} - \frac{1}{2} \cdot 4\right | + \left | \frac{1}{2} \cdot \frac{1}{3} +4\right |$

$= \left | \frac{1}{3} - 2\right | + \left | \frac{1}{6} +4\right |$

$= \left | -1 \frac{2}{3} \right | + \left | 4 \frac{1}{6} \right |$

$= 1 \frac{2}{3} + 4 \frac{1}{6}$

$= 5 \frac{5}{6}$

Report an Error

Example Question #692 : Arithmetic

Define $g(x)= \left | \left | 1,000- \sqrt{x}\right | - x^{3} \right |$ .

Evaluate g(16) .

Possible Answers:

$5\textup{,}092$

$3\textup{,}092$

$5\textup{,}100$

$3\textup{,}100$

$\textup{The expression is undefined.}$

Correct answer:

$3\textup{,}100$

Explanation:

$g(x)= \left | \left | 1,000- \sqrt{x}\right | - x^{3} \right |$

$g(16)= \left | \left | 1,000- \sqrt{16}\right | - 16^{3} \right |$

$= \left | \left | 1,000- 4 \right | - 16^{3} \right |$

$= \left | \left | 996 \right | - 16^{3} \right |$

$= \left | 996 - 16^{3} \right |$

$= \left | 996 - 4,096 \right |$

$= \left | -3,100 \right |$

=3,100

Report an Error

Example Question #243 : Integers

Solve

$\left | x -7\right | = 3$

Possible Answers:

x=10, 4

x=-4

No solution

x=10

x=0

Correct answer:

x=10, 4

Explanation:

Since this is an absolute value equation, we must set the left hand side equal to both the positive and negative versions of the right side. Therefore,

x-7 = 3

x-7 = -3

Solving the first equation, we see that x=10

Solving the second, we see that x=4

When we substitute each value back into the original equation $\left | x -7\right | = 3$ , we see that they both check.

$\left | 10 -7\right | = \left | 3 \right | =3$

$\left | 4 -7\right | = \left | -3 \right | =3$

Report an Error

Example Question #12 : How To Find Absolute Value

Solve:

|4x -2 | = 14

Possible Answers:

x=-3

x=4

None of the given answers.

x=-3, 4

x=-4, 3

Correct answer:

x=-3, 4

Explanation:

To solve this equation, we want to set 4x-2 equal to both and and solve for .

Therefore:

4x-2 = 14

4x = 16

x=4

and

4x-2=-14

4x = -12

x=-3

We can check both of these answers by plugging them back into the inequality to see if the statement is true.

|4(4) -2| = |16 -2| = |14| = 14

and

|4(-3)-2|=|-14| = 14

Both answers check, so our final answer is x=-3, 4

Report an Error

Example Question #884 : Arithmetic

Solve:

$| \frac{x}{2}+\pi | =4\pi$

Possible Answers:

$6\pi, -10\pi$

6, 10

$6\pi, 10\pi$

Correct answer:

$6\pi, -10\pi$

Explanation:

To solve this problem, we want to set what's inside the absolute value signs equal to the positive and negative value on the right side of the equation. That's because the value inside the absolute value symbols could be equivalent to $4\pi$ or $-4\pi$ , and the equation would still hold true.

So let's set $\frac{x}{2}+\pi$ equal to $4\pi$ and $-4\pi$ separately and solve for our unknown.

First:

$\frac{x}{2}+\pi = 4\pi$

$\frac{x}{2}=3\pi$

$x=6\pi$

Second:

$\frac{x}{2}+\pi = -4\pi$

$\frac{x}{2} = -5\pi$

$x=-10\pi$

Therefore, our answers are $6\pi$ and $-10\pi$ .

Report an Error

Example Question #695 : Arithmetic

Evaluate the expression if x=5 and y=7 .

$\left | 4x+3y \right | - \left | 4x-3y \right |$

Possible Answers:

Correct answer:

Explanation:

$\left | 4x+3y \right | - \left | 4x-3y \right |$

To solve, we replace each variable with the given value.

$\left | 4 (5) +3 ( 7) \right | - \left | 4 (5) -3 ( 7) \right |\ .$

$\left | 20 +21 \right | - \left | 20 -21 \right |$

Simplify. Remember that terms inside of the absolute value are always positive.

$\left | 41 \right | - \left | -1 \right |=41-1 = 40$

Report an Error

Example Question #12 : How To Find Absolute Value

Simplify the following:

$\left | 56-107\right |$

Possible Answers:

163

Correct answer:

Explanation:

Simplify the following:

$\left | 56-107\right |$

Begin with basic subtraction:

$\left | 56-107\right |=\left | -51\right |$

Next, remember what we do with absolute value signs; we change negative values to positive values, and positive values remain positive.

$\left | -51\right |=51$

So our answer is positive 51

Report an Error

Example Question #14 : How To Find Absolute Value

Solve for all possible values of x.

$\left | 84x+14\right |=7x-35$

Possible Answers:

$\frac{-7}{11}, \frac{3}{13}$

$\frac{7}{11}$

$\frac{-3}{11}$

$\frac{7}{11}, \frac{-7}{13}$

Correct answer:

$\frac{-7}{11}, \frac{3}{13}$

Explanation:

When solving for x in the presence of absolute value, there are always two answers.

To eliminate the absolute value, the equation must be re-written two ways:

84x+14=7x-35 and 84x+14=-(7x-35)

84x=7x-49 and 84x+14=-7x+35

77x=-49 and 91x+14=35

$x=\frac{-49}{77}$ and 91x = 21

$x=\frac{-7}{11}$ and $x=\frac{3}{13}$

Report an Error

Example Question #693 : Arithmetic

Define an operation $\blacklozenge$ as follows:

For all real numbers a,b ,

$a \blacklozenge b = \left | 2a- 2b + 5 \right |$

Evaluate $(-4) \blacklozenge (-7)$

Possible Answers:

Both and

Correct answer:

Explanation:

$a \blacklozenge b = \left | 2a- 2b + 5 \right |$

$(-4) \blacklozenge (-7) = \left | 2 (-4)- 2(-7) + 5 \right |$

$= \left |-8- (-14) + 5 \right |$

$= \left |-8+14 + 5 \right |$

$= \left |11 \right |$

= 11

Report an Error

View SAT Mathematics Tutors

Aaqib
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Neuroscience.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Zachary
Certified Tutor

Yale University, Bachelor of Science, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

Spanish Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Washington DC, MCAT Courses & Classes in Miami, SAT Courses & Classes in Seattle, ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in New York City, Spanish Courses & Classes in Boston, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in New York City

Popular Test Prep

MCAT Test Prep in Los Angeles, SAT Test Prep in New York City, GMAT Test Prep in San Diego, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Houston, GRE Test Prep in Phoenix, SSAT Test Prep in Phoenix, LSAT Test Prep in Chicago, MCAT Test Prep in Phoenix, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : How to find absolute value

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : Absolute Value

Example Question #1 : How To Find Absolute Value

Example Question #692 : Arithmetic

Example Question #243 : Integers

Example Question #12 : How To Find Absolute Value

Example Question #884 : Arithmetic

Example Question #695 : Arithmetic

Example Question #12 : How To Find Absolute Value

Example Question #14 : How To Find Absolute Value

Example Question #693 : Arithmetic

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: