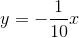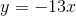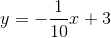We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #531 : Geometry

What is the slope-intercept form of $\dpi{100} \small 8x-2y-12=0$ ?

Possible Answers:

$\dpi{100} \small y=4x+6$

$\dpi{100} \small y=4x-6$

$\dpi{100} \small y=-2x+3$

$\dpi{100} \small y=2x-3$

$\dpi{100} \small y=-4x+6$

Correct answer:

$\dpi{100} \small y=4x-6$

Explanation:

The slope intercept form states that $\dpi{100} \small y=mx+b$ . In order to convert the equation to the slope intercept form, isolate $\dpi{100} \small y$ on the left side:

$\dpi{100} \small 8x-2y=12$

$\dpi{100} \small -2y=-8x+12$

$\dpi{100} \small y=4x-6$

Report an Error

Example Question #1441 : Gre Quantitative Reasoning

A line is defined by the following equation:

7x+28y=84

What is the slope of that line?

Possible Answers:

$-\frac{1}{4}$

$\frac{1}{4}$

Correct answer:

$-\frac{1}{4}$

Explanation:

The equation of a line is

y=mx + b where m is the slope

Rearrange the equation to match this:

7x + 28y = 84

28y = -7x + 84

y = -(7/28)x + 84/28

y = -(1/4)x + 3

m = -1/4

Report an Error

Example Question #101 : Algebra

If the coordinates (3, 14) and (–5, 15) are on the same line, what is the equation of the line?

Possible Answers:

$y=-\frac{1}{8}x+14.375$

$y=\frac{1}{8}x+14.375$

y=-8x+38

$y=-\frac{1}{8}x+13.625$

y=-8x-38

Correct answer:

$y=-\frac{1}{8}x+14.375$

Explanation:

First solve for the slope of the line, m using y=mx+b

m = (y2 – y1) / (x2 – x1)

= (15 – 14) / (–5 –3)

= (1 )/( –8)

=–1/8

y = –(1/8)x + b

Now, choose one of the coordinates and solve for b:

14 = –(1/8)3 + b

14 = –3/8 + b

b = 14 + (3/8)

b = 14.375

y = –(1/8)x + 14.375

Report an Error

Example Question #252 : Geometry

What is the equation of a line that passes through coordinates $\dpi{100} \small (2,6)$ and $\dpi{100} \small (3,5)$ ?

Possible Answers:

$\dpi{100} \small y=-x+8$

$\dpi{100} \small y=2x+4$

$\dpi{100} \small y=2x-4$

$\dpi{100} \small y=3x+2$

$\dpi{100} \small y=x+7$

Correct answer:

$\dpi{100} \small y=-x+8$

Explanation:

Our first step will be to determing the slope of the line that connects the given points.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{6-5}{2-3}=\frac{1}{-1}=-1$

Our slope will be . Using slope-intercept form, our equation will be y=(-1)x+b . Use one of the give points in this equation to solve for the y-intercept. We will use $\dpi{100} \small (2,6)$ .

6=(-1)(2)+b

6=-2+b

8=b

Now that we know the y-intercept, we can plug it back into the slope-intercept formula with the slope that we found earlier.

y=(-1)x+8

y=-x+8

This is our final answer.

Report an Error

Example Question #21 : How To Find The Equation Of A Line

Which of the following equations does NOT represent a line?

Possible Answers:

x+y=10

5y=10

x^2+y=10

x-y=10

x=10

Correct answer:

x^2+y=10

Explanation:

The answer is x^2+y=10 .

A line can only be represented in the form x=z or y=mx+b , for appropriate constants , , and . A graph must have an equation that can be put into one of these forms to be a line.

x^2+y=10 represents a parabola, not a line. Lines will never contain an x^2 term.

Report an Error

Example Question #532 : Geometry

Let y = 3x – 6.

At what point does the line above intersect the following:

$2x =\frac{2}{3}y+4$

Possible Answers:

They do not intersect

(–3,–3)

(–5,6)

They intersect at all points

(0,–1)

Correct answer:

They intersect at all points

Explanation:

If we rearrange the second equation it is the same as the first equation. They are the same line.

Report an Error

Example Question #142 : Lines

Find the equation of a line that goes through the points (0,3) , and (-10,4) .

Possible Answers:

$y=-\frac{1}{10}x$

$y=-\frac{1}{10}x+3$

y=-10x+3

y=-13x

y=-10x

Correct answer:

$y=-\frac{1}{10}x+3$

Explanation:

For finding the equation of a line, we will be using point-slope form, which is

y-y_0=m(x-x_0) , where is the slope, and (x_0, y_0) is a point.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-3}{-10-0}=\frac{1}{-10}=-\frac{1}{10}$

We will pick the point (0,3)

$y-3=-\frac{1}{10}(x-0)$

$y=-\frac{1}{10}x+3$

If we picked the point (-10,4)

$y-4=-\frac{1}{10}(x+10)$

$y=-\frac{1}{10}x-1+4$

$y=-\frac{1}{10}x+3$

We get the same result

Report an Error

Example Question #531 : Sat Mathematics

Find the equation of a line that passes through the point (-2,5) , and is parallel to the line y=-3x+4 .

Possible Answers:

y=-3x-1

y=-3x-10

y=-3x

y=-3x-3

y=-3x+1

Correct answer:

y=-3x-1

Explanation:

Since we want a line that is parallel, we will have the same slope as the line (-3) . We can use point slope form to create an equation.

y-y_0=m(x-x_0) , where is the slope and (x_0, y_0) is a point.

y-5=-3(x-(-2))

y-5=-3(x+2)

y-5=-3x-6

y=-3x-1

Report an Error

Example Question #23 : Slope And Line Equations

Find the equation of the line shown in the graph below:

Sat_math_164_05

Possible Answers:

y = -1/2x - 4

y = x/2 + 4

y = -1/2x + 4

y = 2x + 4

Correct answer:

y = x/2 + 4

Explanation:

Based on the graph the y-intercept is 4. So we can eliminate choice y = x/2 - 4.

The graph is rising to the right which means our slope is positive, so we can eliminate choice y = -1/2x + 4.

Based on the line, if we start at (0,4) and go up 1 then 2 to the right we will be back on the line, meaning we have a slope of (1/2).

Using the slope intercept formula we can plug in y= (1/2)x + 4.

Report an Error

Example Question #1 : Distance Formula

What is the distance between (1, 4) and (5, 1)?

Possible Answers:

Correct answer:

Explanation:

Let P₁ = (1, 4) and P₂ = (5, 1)

Substitute these values into the distance formula:

The distance formula is an application of the Pythagorean Theorem: a² + b² = c²

Report an Error

View SAT Mathematics Tutors

Momeena
Certified Tutor

State University of New York at New Paltz, Bachelors, Mathematics & Elementary Education. State University of New York at New...

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View SAT Mathematics Tutors

Scott
Certified Tutor

Rutgers College, Bachelors, Political Science and Government. Florida Coastal School of Law, PHD, Law.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in San Diego, GRE Courses & Classes in Miami, GMAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Miami, Spanish Courses & Classes in Houston, ISEE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in New York City, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Miami, MCAT Test Prep in Los Angeles, GMAT Test Prep in Miami, SSAT Test Prep in Washington DC, LSAT Test Prep in New York City, SSAT Test Prep in Seattle, SSAT Test Prep in Chicago, LSAT Test Prep in Boston, ISEE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #531 : Geometry

Example Question #1441 : Gre Quantitative Reasoning

Example Question #101 : Algebra

Example Question #252 : Geometry

Example Question #21 : How To Find The Equation Of A Line

Example Question #532 : Geometry

Example Question #142 : Lines

Example Question #531 : Sat Mathematics

Example Question #23 : Slope And Line Equations

Example Question #1 : Distance Formula

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: