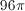Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Solid Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Volume Of A Cylinder

What is the volume of a right cylinder with a circumference of 25π in and a height of 41.3 in?

Possible Answers:

3831.34π in³

4813.33π in³

25812.5π in³

6453.125π in³

1032.5π in³

Correct answer:

6453.125π in³

Explanation:

The formula for the volume of a right cylinder is: V = A * h, where A is the area of the base, or πr². Therefore, the total formula for the volume of the cylinder is: V = πr²h.

First, we must solve for r by using the formula for a circumference (c = 2πr): 25π = 2πr; r = 12.5.

Based on this, we know that the volume of our cylinder must be: π*12.5²*41.3 = 6453.125π in³

Report an Error

Example Question #121 : Solid Geometry

An 8-inch cube has a cylinder drilled out of it. The cylinder has a radius of 2.5 inches. To the nearest hundredth, approximately what is the remaining volume of the cube?

Possible Answers:

462 in³

157.08 in³

391.33 in³

203.34 in³

354.92 in³

Correct answer:

354.92 in³

Explanation:

We must calculate our two volumes and subtract them. The volume of the cube is very simple: 8 * 8 * 8, or 512 in³.

The volume of the cylinder is calculated by multiplying the area of its base by its height. The height of the cylinder is 8 inches (the height of the cube through which it is being drilled). Therefore, its volume is πr²h = π * 2.5²* 8 = 50π in³

The volume remaining in the cube after the drilling is: 512 – 50π, or approximately 512 – 157.0795 = 354.9205, or 354.92 in³.

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

An 12-inch cube of wood has a cylinder drilled out of it. The cylinder has a radius of 3.75 inches. If the density of the wood is 4 g/in³, what is the mass of the remaining wood after the cylinder is drilled out?

Possible Answers:

4791.43 g

4921.4 g

2594.11 g

3813.3 g

3193.33 g

Correct answer:

4791.43 g

Explanation:

We must calculate our two volumes and subtract them. Following this, we will multiply by the density.

The volume of the cube is very simple: 12 * 12 * 12, or 1728 in³.

The volume remaining in the cube after the drilling is: 1728 – 168.75π, or approximately 1728 – 530.1433125 = 1197.8566875 in³. Now, multiply this by 4 to get the mass: (approx.) 4791.43 g.

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

A hollow prism has a base 5 in x 6 in and a height of 10 in. A closed, cylindrical can is placed in the prism. The remainder of the prism is then filled with gel around the cylinder. The thickness of the can is negligible. Its diameter is 4 in and its height is half that of the prism. What is the approximate volume of gel needed to fill the prism?

Possible Answers:

187.73 in³

203.44 in³

237.17 in³

249.73 in³

103.33 in³

Correct answer:

237.17 in³

Explanation:

The general form of our problem is:

Gel volume = Prism volume – Can volume

The prism volume is simple: 5 * 6 * 10 = 300 in³

The volume of the can is found by multiplying the area of the circular base by the height of the can. The height is half the prism height, or 10/2 = 5 in. The area of the base is equal to πr². Note that the prompt has given the diameter. Therefore, the radius is 2, not 4. The base's area is: 2²π = 4π. The total volume is therefore: 4π * 5 = 20π in³.

The gel volume is therefore: 300 – 20π or (approx.) 237.17 in³.

Report an Error

Example Question #2 : How To Find The Volume Of A Cylinder

A hollow prism has a base 12 in x 13 in and a height of 42 in. A closed, cylindrical can is placed in the prism. The remainder of the prism is then filled with gel, surrounding the can. The thickness of the can is negligible. Its diameter is 9 in and its height is one-fourth that of the prism. The can has a mass of 1.5 g per in³, and the gel has a mass of 2.2 g per in³. What is the approximate overall mass of the contents of the prism?

Possible Answers:

139.44 g

973.44 g

11.48 kg

13.95 kg

15.22 kg

Correct answer:

13.95 kg

Explanation:

We must find both the can volume and the gel volume. The formula for the gel volume is:

Gel volume = Prism volume – Can volume

The prism volume is simple: 12 * 13 * 42 = 6552 in³

The volume of the can is found by multiplying the area of the circular base by the height of the can. The height is one-fourth the prism height, or 42/4 = 10.5 in. The area of the base is equal to πr². Note that the prompt has given the diameter. Therefore, the radius is 4.5, not 9. The base's area is: 4.5²π = 20.25π. The total volume is therefore: 20.25π * 10.5 = 212.625π in³.

The gel volume is therefore: 6552 – 212.625π or (approx.) 5884.02 in³.

The approximate volume for the can is: 667.98 in³

From this, we can calculate the approximate mass of the contents:

Gel Mass = Gel Volume * 2.2 = 5884.02 * 2.2 = 12944.844 g

Can Mass = Can Volume * 1.5 = 667.98 * 1.5 = 1001.97 g

The total mass is therefore 12944.844 + 1001.97 = 13946.814 g, or approximately 13.95 kg.

Report an Error

Example Question #11 : How To Find The Volume Of A Cylinder

A vase needs to be filled with water. If the vase is a cylinder that is $\dpi{100} \small 12{}''$ tall with a $\dpi{100} \small 2{}''$ radius, how much water is needed to fill the vase?

Possible Answers:

$\dpi{100} \small 48\pi$

$\dpi{100} \small 12\pi$

$\dpi{100} \small 96\pi$

$\dpi{100} \small 64\pi$

$\dpi{100} \small 24\pi$

Correct answer:

$\dpi{100} \small 48\pi$

Explanation:

Cylinder

$\dpi{100} \small V = \pi r^{2}h$

$\dpi{100} \small V = \pi (2)^{2}\times 12$

$\dpi{100} \small V = 4\times 12\pi$

$\dpi{100} \small V = 48\pi$

Report an Error

Example Question #21 : Cylinders

A cylinder has a base diameter of 12 in and is 2 in tall. What is the volume?

Possible Answers:

$48\pi in^{3}$

$72\pi in^{3}$

$288\pi in^{3}$

$36\pi in^{3}$

$24\pi in^{3}$

Correct answer:

$72\pi in^{3}$

Explanation:

The volume of a cylinder is $V=\pi r^{2}h$

The diameter is given, so make sure to divide it in half.

The units are inches cubed in this example

Report an Error

Example Question #21 : Cylinders

What is the volume of a cylinder with a radius of 4 and a height of 5?

Possible Answers:

$72\pi$

$60\pi$

$54\pi$

$80\pi$

$40\pi$

Correct answer:

$80\pi$

Explanation:

$volume = \pi r^{2}h = \pi \cdot 4^{2} \cdot 5 = 80\pi$

Report an Error

Example Question #12 : How To Find The Volume Of A Cylinder

Claire's cylindrical water bottle is 9 inches tall and has a diameter of 6 inches. How many cubic inches of water will her bottle hold?

Possible Answers:

$81\pi$

$45\pi$

$54\pi$

$18\pi$

$324\pi$

Correct answer:

$81\pi$

Explanation:

The volume is the area of the base times the height. The area of the base is $\pi r^{2}$ , and the radius here is 3. $\pi\cdot 3^{2}\cdot 9=81\pi$

Report an Error

Example Question #13 : Cylinders

What is the volume of a circular cylinder whose height is 8 cm and has a diameter of 4 cm?

Possible Answers:

$12\pi \ cm^{3}$

$64\pi \ cm^{3}$

$128\pi \ cm^{3}$

$32\pi \ cm^{3}$

$16\pi \ cm^{3}$

Correct answer:

$32\pi \ cm^{3}$

Explanation:

The volume of a circular cylinder is given by $V = \pi r^{2}h$ where is the radius and is the height. The diameter is given as 4 cm, so the radius would be 2 cm as the diameter is twice the radius.

Report an Error

View SAT Mathematics Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

View SAT Mathematics Tutors

Daniel
Certified Tutor

Stony Brook University, Bachelors, Biology, General. SUNY College of Optometry, PHD, Optometry.

View SAT Mathematics Tutors

Danielle
Certified Tutor

Penn State University, Bachelor of Science, Civil Engineering.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Miami, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Chicago, GMAT Courses & Classes in Seattle, ISEE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix, Spanish Courses & Classes in Houston, Spanish Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in Washington DC, GMAT Test Prep in Seattle, MCAT Test Prep in San Diego, MCAT Test Prep in Miami, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Los Angeles, SSAT Test Prep in Chicago, ISEE Test Prep in Houston, SSAT Test Prep in Los Angeles, SSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Solid Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #121 : Solid Geometry

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #2 : How To Find The Volume Of A Cylinder

Example Question #11 : How To Find The Volume Of A Cylinder

Example Question #21 : Cylinders

Example Question #21 : Cylinders

Example Question #12 : How To Find The Volume Of A Cylinder

Example Question #13 : Cylinders

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: