All SAT Math Resources
Example Questions
Example Question #4 : How To Simplify A Fraction
Simplify:
None of the other answers
With this problem the first thing to do is cancel out variables. The x2 can all be divided by each other because they are present in each system. The equation will now look like this:
Now we can see that the equation can all be divided by y, leaving the answer to be:
Example Question #11 : Algebraic Fractions
Simplify the given fraction:
120 goes into 6000 evenly 50 times, so we get 1/50 as our simplified fraction.
Example Question #5 : How To Simplify A Fraction
Simplify the given fraction:
125 goes into 2000 evenly 16 times. 1/16 is the fraction in its simplest form.
Example Question #12 : Algebraic Fractions
Simplify the following expression:
Following this equation, you divide 4 by 8 to get 1/2. When a variable is raised to an exponent, and you are dividing, you subtract the exponents, so 6 – 3 = 3.
Example Question #2518 : Act Math
Reduce the fraction:
The numerator and denominator are both divisible by 12. Thus, we divide both by 12 to get our final answer.
If we instead divide by another common factor, we may need to complete the process again to make sure that we have completely reduced the fraction.
In mathematical words we get the following:
Example Question #15 : Algebraic Fractions
Simplify the fraction:
Break up the fraction into common factors.
Rewrite the fraction.
Cancel the six.
The correct reduced fraction is 
Example Question #16 : Algebraic Fractions
Simplify the fraction:
Break up the fraction into common factors.
Rewrite the fraction.
Cancel the three on the numerator and denominator.
The fraction becomes:
The correct reduced fraction is 
Example Question #17 : Algebraic Fractions
Simplify the following fraction.
In order to simplify the fraction, you need to cancel out everything that the numerator and denominator share. Let's separate it into four sections: the numbers, the variable a, the variable b, and the variable c.
With the variable a, you have
which simplifies to

With the variable b, you have
which simplifies to

With the variable c, you have
which simplifies to

Once you combine everything, you get
Example Question #1 : How To Evaluate A Fraction
Evaluate the following equation when 
1. Plug in 

2. Perform the above operations.
Example Question #1 : How To Evaluate A Fraction
If 

To raise 


All SAT Math Resources



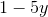





































































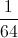




![w^\frac{2}{3}=\sqrt[3]{w^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177545/gif.latex)
![(\frac{1}{8})^\frac{2}{3}=\sqrt[3]{(\frac{1}{8})^2}=\sqrt[3]{\frac{1}{64}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177546/gif.latex)
![\sqrt[3]{\frac{1}{64}}=\frac{1}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177547/gif.latex)




