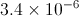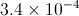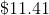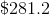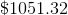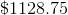All SAT Math Resources
Example Questions
Example Question #3 : How To Use Scientific Notation
Convert from decimal to scientific notation:
In this case you have to move the decimal point 6 places to the right. When you move the decimal point to the right the exponent becomes negative. Similarly when you move the decimal point to the left the exponent is positive. Also, to the left of the decimal place there can be only one digit.
Example Question #241 : Exponents
What is the result when 


First, when we round to the nearest thousand we get 5, 679, 000 since we round up when the next digit is greater than 5.
Then, to put it in scientific notation, we arrange the digits so that a decimal point creates a number between 1 and 10. We get 5.679.
Then, we want the exponent of the 10 to be the number of times the decimal needs to move to the right. This is 6 times.
Thus, we get our answer. 
Example Question #12 : How To Use Scientific Notation
What is 
In order to write a number in scientific notation, you must shift the number of decimal places to get a number in the ones place.
Since the original number is a decimal, the exponent will need to be negative. This eliminates three answer choices.
In order to get 
Therefore, the final answer in scientific notation is 
Example Question #7 : How To Use Scientific Notation
Express 0.00000956 in scientific notation.
None of the given answers.
In scientific notation, we want one digit in the unit's place, followed by a decimal point and subsequent digits.
The exponent of 10 is the number of units the decimal point has been shifted.
For 0.00000956, we want to move the decimal over so that we get the number 9.56 times 10 to some power. To do this, we must move the decimal over 6 places. Since 0.00000956 is obviously smaller than 9.56, that means that our exponent must be negative.
Therefore, our answer is 
Example Question #8 : How To Use Scientific Notation
Expand the following number that is written here in scientific notation:
To expand our number, we should look at the exponent provided. We see that our exponent raises 


Example Question #9 : How To Use Scientific Notation
Express 
None of the given answers
To put a number in scientific notation, we want to have a number with one digit in the units place followed by a decimal point and any subsequent digits. That number is then multiplied by ten raised to a power that matches how many places we moved the decimal point in the original number.
To write this number in scientific notation, we want our expression to be 


Therefore, this number in scientific notation is 
Example Question #10 : How To Use Scientific Notation
Which of the following is equivalent to ?
Which of the following is equivalent to ?
To solve this problem, all we need to do is move the decimal point.
Because we have a negative exponent (-3), we have to move our decimal point to the left.
Because our exponent is 3, we will move the decimal point 3 to the left:
Making our answer:
Example Question #1 : How To Find Compound Interest
A five-year bond is opened with 

Each year, you can calculate your interest by multiplying the principle (

For two years, it would be:

Therefore, you can solve for a five year period by doing:
Using your calculator, you can expand the 


Example Question #3 : How To Find Compound Interest
If a cash deposit account is opened with 

It is easiest to break this down into steps. For each year, you will multiply by 
After year 1: 
After year 2: 

After year 3: 

Thus, the positive difference of the interest from the last period and the interest from the first period is:
Example Question #2 : How To Find Compound Interest
Jack has 



First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).
Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:
Plug in the values given:
Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:
Add the two together, and we see that Jack makes a total of, 
Certified Tutor
All SAT Math Resources