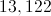We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Exponents

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2191 : Sat Mathematics

If $\sqrt{x}=y^{2}=6$ , then which of the following is equivalent to $x^3y^4$ ?

Possible Answers:

6^4

6^6

6^8

6^7

$6^{8}$

Correct answer:

$6^{8}$

Explanation:

We can break up the equation into two smaller equations involving only x and y. Then, once we solve for x and y, we can find the value of $x^3y^4$ .

Simp_sqrt1

Report an Error

Example Question #11 : How To Multiply Exponents

If $y^7x^8z^2 <0$ which of the following must be true?

I. yx<0

II. yz<0

III. xz<0

Possible Answers:

None

All

III

Correct answer:

None

Explanation:

must be negative because it has an odd power and and have even powers above. But and could be positive or negative, so none of the scenarios has to be true.

Report an Error

Example Question #12 : How To Multiply Exponents

$-\left ( \frac{-1}{3} \right )^{2}$

Possible Answers:

$\frac{1}{3}$

$-\frac{1}{3}$

$\frac{2}{6}$

$-\frac{1}{9}$

$\frac{1}{9}$

Correct answer:

$-\frac{1}{9}$

Explanation:

$= \frac{\left ( -1 \right )^{2}}{\left ( 3 \right )^{2}}$

$= \frac{1}{9}$

Hence the correct answer will be $- \frac{1}{9}$

Report an Error

Example Question #13 : How To Multiply Exponents

Solve for :

$\left ( x \right )^{\frac{3}{5}} = 8$

Possible Answers:

$\frac{1}{8}$

$\frac{1}{32}$

Correct answer:

Explanation:

$\left ( x \right )^{\frac{3}{5}} = 8$

Then

$\left \left ((x \right ) ^{\frac{3}{5}} \right )^{\frac{5}{3}} = 8^{\frac{5}{3}}$

$8^{\frac{5}{3}} = 32$ and $\left ( \left ( x \right ) ^{\frac{3}{5}}\right )^{\frac{5}{3}} = x$

Hence x=32

Report an Error

Example Question #11 : Exponential Operations

(x^3y^6z)(x^2yz^3)=

Possible Answers:

x^5y^7z^3

x^5y^7z^4

x^3y^6z^3

x^6y^6z^3

x^2y^7z^3

Correct answer:

x^5y^7z^4

Explanation:

(x³y⁶z)(x²yz³)

The paraentheses are irrelevant. Rearrange to combine like terms.

x³x²y⁶y¹z¹z³

When you multiply variables with exponents, simply add the exponents together.

x³⁺²y⁶⁺¹z¹⁺³

x⁵y⁷z⁴

Report an Error

Example Question #12 : Exponential Operations

If an original bacteria colony contains six organisms, and triples every hour, how many organisms are there after 7 hours?

Possible Answers:

4374

107,008

13,122

39,366

Correct answer:

13,122

Explanation:

To find the answer we can apply the equation of population $P=6\cdot 3^{n}$ where is the number of hours.

Report an Error

Example Question #13 : Exponential Operations

Simplify: $2a^{2}b(ab^{2} - a^{2}b)$

Possible Answers:

$2a^{3}b^{3} + a^{2}b^{2}$

$ab^{2} - a^{2}b$

$2ab^{2} - 2a^{2}b$

$2a^{3}b^{3} - 2a^{4}b^{2}$

$2a^{2}b + 2a^{4}b^{2}$

Correct answer:

$2a^{3}b^{3} - 2a^{4}b^{2}$

Explanation:

Use the distributive property: $a(b+c)=ab+ac$ . When we multiply variables with exponents, we keep the same base and add the exponents: $a^{m}a^{n} = a^{m+n}$

Report an Error

Example Question #11 : Exponential Operations

Simplify:

$(6x^{2})^{2}\times y^{2} + xyz =$

Possible Answers:

$36x^{5}y^{3}z$

$36x^{4}y^{2}$

$\textbf{cannot be simplified}$

$6x^{4}y^{2}z + xyz$

$36x^{4}y^{2}+xyz$

Correct answer:

$36x^{4}y^{2}+xyz$

Explanation:

$(6x^{2})^{2} = 6^{2}x^{4} = 36x^{4}$

$36x^{4}\times y^{2} = 36x^{4}y^{2}$

We cannot combine $36x^{4}y^{2}$ with $xyz$ , so $(6x^{2})^{2}\times y^{2} + xyz =36x^{4}y^{2}+xyz$ .

Report an Error

Example Question #15 : Exponential Operations

If c^2=15 , then what is the value of c^4 ?

Possible Answers:

110

125

225

$\sqrt{15}$

Correct answer:

225

Explanation:

c⁴ is equal to (c²)(c²).

We know c² = 15. Plugging in this value gives us c⁴ = (15)(15) = 225.

Report an Error

Example Question #2206 : Sat Mathematics

If and are nonzero numbers such that a^2 = b^3 , which of the following is equivalent to a^6 ?

Possible Answers:

b^6

$b^{11}$

b^8

b^9

b^7

Correct answer:

b^9

Explanation:

For this problem, we need to make use of the property of exponents, which states that (x^y)^z = x^y^z.

We are given a² but are asked to find a⁶.

Let's raise both sides of the equation to the third power, so that we will end up with a⁶ on the left side.

(a²)³ = (b³)³

Now, according to the property of exponents mentioned before, we can multiply the exponents.

a^(2*3) = b^(3*3)

a⁶ = b⁹

The answer is b⁹.

Report an Error

View SAT Mathematics Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Miami, ISEE Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in New York City, SAT Courses & Classes in Houston, Spanish Courses & Classes in Philadelphia, ISEE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Houston, Spanish Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in Phoenix, MCAT Test Prep in Miami, ACT Test Prep in Denver, SSAT Test Prep in Houston, SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, SAT Test Prep in New York City, SSAT Test Prep in New York City, MCAT Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Exponents

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #2191 : Sat Mathematics

Example Question #11 : How To Multiply Exponents

Example Question #12 : How To Multiply Exponents

Example Question #13 : How To Multiply Exponents

Example Question #11 : Exponential Operations

Example Question #12 : Exponential Operations

Example Question #13 : Exponential Operations

Example Question #11 : Exponential Operations

Example Question #15 : Exponential Operations

Example Question #2206 : Sat Mathematics

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: