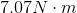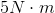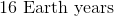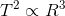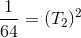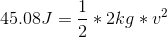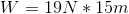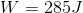All SAT II Physics Resources
Example Questions
Example Question #1 : Kinematics Equations

If the block of mass 



Begin by making a free body diagram for each block:

Use the diagram to write an equation for net force on each block:
Since 

Then add the equations to get:
Next rearrange to isolate 
Substitute the given values from the question and solve:
Example Question #11 : Sat Subject Test In Physics
A 


What is the force due to friction?
Since there is only one force acting upon the object, the force due to friction, we can find its value using the equation 
Start by finding the initial velocity. The problem gives us distance, final velocity, and change in time. We can use these values in the equation below to solve for the initial velocity.
Plug in our given values and solve.
We can use a linear motion equation to solve for the acceleration, using the velocity we just found. We now have the distance, time, and initial velocity.
Plug in the given values to solve for acceleration.
Now that we have the acceleration and the mass, we can solve for the force of friction.

Example Question #11 : Sat Subject Test In Physics
If the distance between two objects is reduced by two-thirds, how will the gravitational force between the objects be affected?
Decreases by a factor of
Increases by a factor of
Decreases by a factor of
Increases by a factor of
Increases by a factor of
Increases by a factor of
According to Newton's law of universal gravitation, the gravitational force between two objects is inversely proportional to the square of the distance between them.
If the distance is reduced by two-thirds, then the final distance is equal to one-third the original distance.
Using this term in the equation will show that the force increases by a factor of nine.
Example Question #291 : High School Physics
A 

There are two forces at work here: the force due to gravity and the restoring force of the spring. We can set these two forces equal to one another because the forces must be in equilibrium when the spring is compressed at its maximum point.
Expand this equation by using the formulas for gravitational and spring force, respectively.
Plug in our given values for the girl's mass, gravitational acceleration, and the spring constant. Using these values, we can solve for the displacement of the spring.
Example Question #1 : Spring Force
A certain spring has an equilibrium length of 


The equation for spring force is:
The force applied to the spring will be equal and opposite the force of the spring itself. In this case, the force applied is 

The change in distance will be 

Example Question #1 : Other Mechanical Forces
A wrench is being used to tighten a bolt. The center of the bolt is the pivot point, and the wrench is 

The equation for torque is
The force is applied 
Example Question #11 : Mechanics
Suppose a planet has a mean distance from the sun four times that of Earth's. How many Earth years would it take this planet to orbit the sun?
Kepler's third law gives the relationship between the period of a planet's orbit (year) and the radius of its orbit (distance form the sun):
The square of the period is proportional to the cube of the radius. We can set the product of these values equal to a constant, since they are proportional.
In our question, we know that the distance is increased by a factor of four and the period for Earth is 1 year.
Solve for the period of the new planet.
The period for the new planet is one-eighth the period of Earth, meaning that in one Earth year this planet will complete only one-eighth its orbit. It will take eight Earth years to equal one complete orbit for this planet.
Example Question #11 : Sat Subject Test In Physics
A 
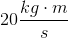
Linear momentum is calculated as the product of mass and velocity:
We are given the mass of the cart and its momentum, allowing us to solve for its velocity.
Now that we know the velocity of the cart, we need to use the equation for kinetic energy:
Use the value of the velocity and the given mass of the cart to solve.
Example Question #13 : Sat Subject Test In Physics
A 

The relationship between velocity and energy is:
We know the mass, but we need to find the total kinetic energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 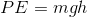
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.
Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.
Example Question #1 : Calculating Work
A 


The formula for work is:
Given the values for force and distance, we can calculate the work done.
Note that no work is done by the force of gravity or the weight of the box, since the vertical position does not change.
Certified Tutor
Certified Tutor
All SAT II Physics Resources