All SAT II Math II Resources
Example Questions
Example Question #4 : Graphing Piecewise And Recusive Functions
Define a function as follows:
At which of the following values of is discontinuous?
I)
II)
III)
I and II only
II and III only
I and III only
None of I, II, and III
All of I, II, and III
I and III only
To determine whether is continuous at , we examine the definitions of on both sides of , and evaluate both for :
evaluated for :
evaluated for :
Since the values do not coincide, is discontinuous at .
We do the same thing with the other two boundary values 0 and .
evaluated for :
evaluated for :
Since the values coincide, is continuous at .
turns out to be undefined for , (since is undefined), so is discontinuous at .
The correct response is I and III only.
Example Question #5 : Graphing Piecewise And Recusive Functions
Define a function as follows:
At which of the following values of is the graph of discontinuous?
I)
II)
III)
None of I, II, and III
All of I, II, and III
I and III only
II and III only
I and II only
II and III only
To determine whether is continuous at , we examine the definitions of on both sides of , and evaluate both for :
evaluated for :
evaluated for :
Since the values coincide, the graph of is continuous at .
We do the same thing with the other two boundary values 0 and 1:
evaluated for :
evaluated for :
Since the values do not coincide, the graph of is discontinuous at .
evaluated for :
evaluate for :
Since the values do not coincide, the graph of is discontinuous at .
II and III only is the correct response.
Example Question #2 : Graphing Piecewise And Recusive Functions
Define a function as follows:
Give the -intercept of the graph of the function.
The graph does not have a -intercept.
To find the -intercept, evaluate using the definition of on the interval that includes the value 0. Since
on the interval ,
evaluate:
The -intercept is .
Example Question #11 : Graphing Functions
Give the period of the graph of the equation
The period of the graph of a cosine function is , or
Since , the period is
Example Question #1 : Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. , , and and are right angles. What percent of is colored red?
, as the length of the altitude corresponding to the hypotenuse, is the geometric mean of the lengths of the parts of the hypotenuse it forms; that is, it is the square root of the product of the two:
.
The area of , the shaded region, is half the products of its legs:
The area of is half the product of its hypoteuse, which we can see as the base, and the length of corresponding altitude :
comprises
of .
Example Question #301 : Sat Subject Test In Math Ii

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a square garden (in green) surrounded by a dirt path (in orange). The dirt path is seven feet wide throughout. What is the area of the dirt path in square feet?
The area of the dirt path is the area of the outer square minus that of the inner square.
The outer square has sidelength 75 feet and therefore has area
square feet.
The inner square has sidelength feet and therefore has area
square feet.
Subtract to get the area of the dirt path:
square feet.
Example Question #3 : Geometry

Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange). The dirt path is six feet wide throughout. Which of the following polynomials gives the area of the garden in square feet?
The length of the garden is feet less than that of the entire lot, or
;
The width of the garden is less than that of the entire lot, or
;
The area of the garden is their product:
Example Question #1 : Geometry

The above figure is a regular decagon. If , then to the nearest whole number, what is ?
As an interior angle of a regular decagon, measures
.
.
can be found using the Law of Cosines:
Example Question #3 : Geometry

The circle in the above diagram has its center at the origin. To the nearest tenth, what is the area of the pink region?
First, it is necessary to determine the radius of the circle. This is the distance between and , so we apply the distance formula:
Subsequently, the area of the circle is
Now, we need to find the central angle of the shaded sector. This is found using the relationship
Using a calculator, we find that ; since we want a degree measure between and , we adjust by adding , so
The area of the sector is calculated as follows:
Example Question #1 : Area
You own a mug with a circular bottom. If the distance around the outside of the mug's base is what is the area of the base?
You own a mug with a circular bottom. If the distance around the outside of the mug's base is what is the area of the base?
Begin by solving for the radius:
Next, plug the radius back into the area formula and solve:
So our answer is:
All SAT II Math II Resources



















































































![(-\pi, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248040/gif.latex)







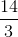


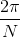
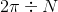




















































![m \angle B = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/217578/gif.latex)








































