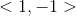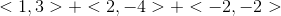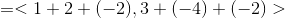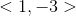We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : SAT Subject Test in Math II

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Sequences

A geometric sequence begins as follows:

6 , i ,...

Give the next term of the sequence.

Possible Answers:

-6 + 2i

6 - i

$\frac{1}{6}$

6+ i

$-\frac{1}{6}$

Correct answer:

$-\frac{1}{6}$

Explanation:

The common ratio of a geometric sequence is the quotient of the second term and the first:

$r = \frac{a_{2}}{a_{1}}= \frac{i}{6} = \frac{1}{6} i$

Multiply the second term by the common ratio to obtain the third term:

$a_{3} = r a_{2} = \frac{1}{6} i \cdot i = \frac{1}{6} \cdot i^{2}= \frac{1}{6} (-1)= -\frac{1}{6}$

Report an Error

Example Question #141 : Sat Subject Test In Math Ii

A geometric sequence begins as follows:

$0.8 , \frac{6}{7} ...$

Give the next term of the sequence.

Possible Answers:

$\frac{32}{35}$

$\frac{8}{9}$

$\frac{45}{49}$

$1 \frac{3}{25}$

Correct answer:

$\frac{45}{49}$

Explanation:

Rewrite the first term as a fraction:

$0.8 = \frac{8}{10} = \frac{4}{5}$

The common ratio of a geometric sequence can be found by dividing the second term by the first, so

$r = \frac{6}{7} \div \frac{4}{5} = \frac{6}{7} \cdot \frac{5}{4} = \frac{15}{14 }$

The third term is equal to the second term multiplied by this common ratio:

$\frac{6}{7} \cdot \frac{15}{14 } = \frac{45}{49}$ .

Report an Error

Example Question #1 : Sequences

A geometric sequence begins as follows:

1+ i, 2, ...

Give the next term of the sequence.

Possible Answers:

3- i

4 - i

2 - 2i

2+ 2i

4+i

Correct answer:

2 - 2i

Explanation:

The common ratio of a geometric sequence is the quotient of the second term and the first:

$r = \frac{a_{2}}{a_{1}}= \frac{2}{1+i }$

Multiply this common ratio by the second term to get the third term:

$a_{3} =r \cdot a_{2} = \frac{2}{1+i } \cdot 2 = \frac{4}{1+i }$

This can be expressed in standard form by rationalizing the denominator; do this by multiplying numerator and denominator by the complex conjugate of the denominator, which is 1 - i :

$\frac{4}{1+i }$

$= \frac{4(1-i)}{(1+i) (1-i) }$

$= \frac{4(1-i)}{1^{2}-i^{2}}$

$= \frac{4(1-i)}{1-(-1)}$

$= \frac{4(1-i)}{2}$

= 2(1-i)

= 2- 2i

Report an Error

Example Question #1 : Sequences

A geometric sequence begins as follows:

$\sqrt{40} , - \sqrt{120},...$

Express the next term of the sequence in simplest radical form.

Possible Answers:

$-2 \sqrt{70}$

$6 \sqrt{10}$

$10 \sqrt{2}$

Correct answer:

$6 \sqrt{10}$

Explanation:

The common ratio of a geometric sequence is the quotient of the second term and the first. Using the Quotient of Radicals property, we can obtain:

$r = \frac{a_{2}}{a_{1}}= \frac{ -\sqrt{120}}{ \sqrt{40}} = - \sqrt{\frac{120}{40}} = -\sqrt{3}$

Multiply the second term by the common ratio, then simplify using the Product Of Radicals Rule, to obtain the third term:

$a_{3} = r a_{2}$

$=-\sqrt{ 3 }\cdot( - \sqrt{120} )$

$= \sqrt{ 3 }\cdot\sqrt{120}$

$= \sqrt{360 }$

$= \sqrt{36} \cdot \sqrt{10 }$

$= 6 \sqrt{10}$

Report an Error

Example Question #2 : Sequences

The first and second terms of a geometric sequence are $\sqrt[3]{16}$ and $\sqrt[3]{48}$ , respectively. In simplest form, which of the following is its third term?

Possible Answers:

$2 \sqrt[3]{18}$

$2 \sqrt[3]{10}$

$4 \sqrt[3]{5}$

Correct answer:

$2 \sqrt[3]{18}$

Explanation:

The common ratio of a geometric sequence can be determined by dividing the second term by the first. Doing this and using the Quotient of Radicals Rule to simplfy:

$r = \frac{ a_{2}}{ a_{1}} = \frac{ \sqrt[3]{48}}{ \sqrt[3]{16}} = \sqrt[3]{ \frac{48}{16}} = \sqrt[3]{3}$

Multiply this by the second term to get the third term, simplifying using the Product of Radicals Rule

$a_{3} = r a_{2} = \sqrt[3]{3} \cdot \sqrt[3]{48}= \sqrt[3]{144} = \sqrt[3]{8} \cdot \sqrt[3]{18} = 2 \sqrt[3]{18}$

Report an Error

Example Question #141 : Sat Subject Test In Math Ii

An arithmetic sequence begins as follows:

$\frac{5}{12}, 0.45,...$

Give the tenth term.

Possible Answers:

$\frac{3}{4}$

$\frac{2}{3}$

$\frac{7}{10}$

$\frac{11}{15}$

$\frac{43}{60}$

Correct answer:

$\frac{43}{60}$

Explanation:

Rewrite 0.45 as a fraction:

$0.45 = \frac{45}{100} = \frac{9}{20}$

The common difference of an arithmetic sequence can be found by subtracting the first term from the second:

$d = a_{2} - a_{1} = \frac{9}{20} - \frac{5}{12} = \frac{27}{60} - \frac{25}{60} = \frac{2}{60} = \frac{1}{30}$

The th term of an arithmetic sequence can be found using the formula

$a_{n} = a_{1} + (n-1)d$ .

Setting $n = 10, a_{1} = \frac{5}{12} , d = \frac{1}{30}$ :

$a_{10} = \frac{5}{12} + (10-1) \cdot \frac{1}{30}$

$= \frac{5}{12} + 9 \cdot \frac{1}{30}$

$= \frac{5}{12} + \frac{3}{10}$

$= \frac{25}{60} + \frac{18}{60}$

$= \frac{43}{60}$ ,

the correct response.

Report an Error

Example Question #112 : Mathematical Relationships

An arithmetic sequence begins as follows:

$\frac{3}{4} , \frac{13}{16} , \frac{7}{8},...$

Give the eighteenth term of the sequence.

Possible Answers:

$1\frac{7}{8}$

$1 \frac{13}{16}$

$1\frac{3}{4}$

$1\frac{15}{16}$

Correct answer:

$1 \frac{13}{16}$

Explanation:

The common difference of an arithmetic sequence can be found by subtracting the first term from the second:

$d= a_{2} - a_{1}$

Setting $a_{1} = \frac{3}{4}, a_{2} = \frac{13}{16}$ :

$d = \frac{13}{16} - \frac{3}{4} = \frac{13}{16} - \frac{12}{16} = \frac{1 }{16}$

The th term of an arithmetic sequence can be calculated using the formula

$a_{n} = a_{1} + (n- 1)d$

The eighteenth term can be found by setting $a_{1} = \frac{3}{4} = \frac{12}{16},n = 18, d = \frac{1 }{16}$ and evaluating:

$a_{18} = \frac{12}{16} + (18- 1) \frac{1}{16}$

$= \frac{12}{16}+ 17 \cdot \frac{1}{16}$

$= \frac{12}{16} + 17 \cdot \frac{1}{16}$

$= \frac{12}{16} + \frac{17}{16}$

$= \frac{29}{16}$

$=1 \frac{13}{16}$

Report an Error

Example Question #1 : Vectors

Add the vectors: <1,3> + <2,-4> +< -2,-2>

Possible Answers:

<-1,-3>

<1,-1>

<1,-3>

<-5,-9>

<5,-9>

Correct answer:

<1,-3>

Explanation:

Combine the values as one vector.

<1,3> + <2,-4> +< -2,-2>

= <1+2+(-2), 3+(-4)+(-2)>

Combine the terms.

The answer is: <1,-3>

Report an Error

Example Question #1 : Other Mathematical Relationships

Add in modulo 9:

5 + 6 + 5 + 4 + 3

Possible Answers:

Correct answer:

Explanation:

In modulo 9 arithmetic, a number is congruent to the remainder of its division by 9.

Since

5 + 6 + 5 + 4 + 3 = 23

and

$23 \div 9 = 2\textrm{ R }5$ ,

$5 + 6 + 5 + 4 + 3 \equiv 5 \mod 9$ ,

making "5" the correct response.

Report an Error

Example Question #149 : Sat Subject Test In Math Ii

varies directly as and inversely as .

If T = 273 and P = 100 , then V = 1,000 .

To the nearest whole number, evaluate if T = 293 and P = 110 .

Possible Answers:

Insufficient information is given to answer the question.

$V \approx 976$

$V \approx 909$

$V \approx 1,073$

$V \approx 1,025$

Correct answer:

$V \approx 976$

Explanation:

varies directly as and inversely as . This means that for some constant of variation ,

$\frac{V P }{T } = k$

Alternatively,

$\frac{V_{1}P_{1}}{T_{1}} = \frac{V_{2}P_{2}}{T_{2}}$

We can substitute the initial conditions for thevariables on the left side and the final conditions for those on the right side, then solve for $V_{2}$ :

$\frac{1,000 \cdot 100}{273} = \frac{V_{2} \cdot 110}{293}$

$\frac{V_{2} \cdot 110}{293} \cdot \frac{293}{ 110} = \frac{1,000 \cdot 100}{273} \cdot \frac{293}{ 110}$

$V_{2} = \frac{1,000 \cdot 100 \cdot 293}{273\cdot 110} \approx 976$

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Rodolfo
Certified Tutor

The University of Texas at San Antonio, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 2 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 2 Tutors

Brianna
Certified Tutor

Cedarville University, Bachelor of Science, Civil Engineering.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Washington DC, Statistics Tutors in New York City, Math Tutors in San Diego, LSAT Tutors in Dallas Fort Worth, English Tutors in San Diego, GRE Tutors in Dallas Fort Worth, Physics Tutors in Washington DC, Physics Tutors in Chicago, Physics Tutors in Philadelphia, Statistics Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Houston, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Houston, GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in San Diego, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston, Spanish Courses & Classes in Seattle, SAT Courses & Classes in Phoenix

Popular Test Prep

MCAT Test Prep in New York City, GMAT Test Prep in Miami, SSAT Test Prep in San Diego, GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Seattle, GMAT Test Prep in Washington DC, GRE Test Prep in Boston, ISEE Test Prep in Denver, GRE Test Prep in Denver, ACT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : SAT Subject Test in Math II

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Sequences

Example Question #141 : Sat Subject Test In Math Ii

Example Question #1 : Sequences

Example Question #1 : Sequences

Example Question #2 : Sequences

Example Question #141 : Sat Subject Test In Math Ii

Example Question #112 : Mathematical Relationships

Example Question #1 : Vectors

Example Question #1 : Other Mathematical Relationships

Example Question #149 : Sat Subject Test In Math Ii

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: