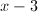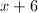Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Simplifying Expressions

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Single Variable Algebra

Decrease 6y + 17 by 30%. Which of the following will this be equal to?

Possible Answers:

1.8y +5.1

4.2y + 17

4.2y + 11.9

6y-13

The correct answer is not among the other responses.

Correct answer:

4.2y + 11.9

Explanation:

A number decreased by 30% is equivalent to 100% of the number minus 30% of the number. This is taking 70% of the number, or, equivalently, multiplying it by 0.7.

Therefore, 6y + 17 decreased by 30% is 0.7 times this, or

$0.7 \left (6y + 17 \right ) = 0.7 \cdot 6y +0.7 \cdot 17 = 4.2y + 11.9$

Report an Error

Example Question #12 : Simplifying Expressions

The polynomial $x^{4} - 27x^{2}+ 5x - A$ is divisible by the linear binomial x - 6 . Evaluate .

Possible Answers:

A = 354

A = - 354

None of the other choices gives the correct answer.

A =-294

A =294

Correct answer:

A = 354

Explanation:

By the factor theorem, a polynomial p (x) is divisible by the linear binomial x - c if and only if p(c) = 0 . Therefore, we want the value of that makes the polynomial equal to 0 when evaluated at x = 6 .

$x^{4} - 27x^{2}+ 5x - A = 0$

$6^{4} - 27 \cdot 6^{2}+ 5 \cdot 6 - A = 0$

$1,296- 27 \cdot 36+ 30- A = 0$

1,296- 972+ 30- A = 0

354- A = 0

354=A

Report an Error

Example Question #13 : Simplifying Expressions

Factor:

$125T^{3}+729$

Possible Answers:

$(5T+9)(5T-9)^{2}$

$(5T+9)(25T^{2}+81)$

$(5T+9)(25T^{2}-45T +81)$

$(5T+9)^{3}$

$(5T+9)(25T^{2}+45T +81)$

Correct answer:

$(5T+9)(25T^{2}-45T +81)$

Explanation:

$125T^{3}+729$ can be rewritten as $(5T)^{3} + 9^{3}$ and is therefore the sum of two cubes. As such, it can be factored using the pattern

$A^{3}+B^{3} =(A+B) (A^{2}-AB +B^{2})$

where A = 5T, B = 9 .

$125T^{3}+729$

$=(5T)^{3} + 9^{3}$

$= (5T+9)[(5T)^{2}-5T \cdot 9 +9^{2}]$

$= (5T+9)(25T^{2}-45T +81)$

Report an Error

Example Question #271 : Sat Subject Test In Math I

Factor completely:

$t^{3} +4t^{2}-9t -36$

Possible Answers:

$\left (t ^{2}+6 \right ) \left (t-6} \right )$

$\left (t ^{2}-6 \right ) \left (t+6} \right )$

$\left (t +3 \right )^{2} \left (t -4} \right )$

$\left (t -3 \right ) \left (t +3 \right ) \left (t + 4} \right )$

$\left (t ^{2}+9 \right ) \left (t-4} \right )$

Correct answer:

$\left (t -3 \right ) \left (t +3 \right ) \left (t + 4} \right )$

Explanation:

The grouping technique works here:

$t^{3} +4t^{2}-9t -36$

$=\left (t^{3} +4t^{2} \right )-\left (9t +36 \right )$

$=\left (t ^{2} \cdot t +t^{2} \cdot 4} \right )-\left (9 \cdot t +9 \cdot 4 \right )$

$=t ^{2} \left (t + 4} \right )-9 \left ( t + 4 \right )$

$=\left (t ^{2}-9 \right ) \left (t + 4} \right )$

The first factor is the difference of squares and can be factored further accordingly:

$\left (t ^{2}-9 \right ) \left (t + 4} \right )$

$=\left (t ^{2}- 3^{2} \right ) \left (t + 4} \right )$

$=\left (t -3 \right ) \left (t +3 \right ) \left (t + 4} \right )$

Report an Error

Example Question #272 : Sat Subject Test In Math I

Factor completely:

$t^{3} - 243$

Possible Answers:

$(t - 3)\left ( t^{2}+ 3t + 81\right )$

The polynomial is prime.

$(t - 3)(t-9) ^{2}$

$(t - 3)\left ( t^{2} + 81\right )$

$(t - 3)\left ( t^{2}+9t + 81\right )$

Correct answer:

The polynomial is prime.

Explanation:

Since the first term is a perfect cube, the factoring pattern we are looking to take advantage of is the difference of cubes pattern. However, 243 is not a perfect cube of an integer $(6^{3} = 216 < 243 < 7^{3} = 343)$ , so the factoring pattern cannot be applied. No other pattern fits, so the polynomial is a prime.

Report an Error

Example Question #122 : Single Variable Algebra

Exponentiate:

$\left (x^{2} + x + 7 \right )^{2}$

Possible Answers:

$x^{4} + x^{2} + 49$

$x^{4} + 2x^{3} +15x^{2} + 14x+ 49$

$x^{4} + 2x^{3} +8x^{2} + 14x+ 14$

$x^{4} + x^{3} +15x^{2} + 14x+ 49$

$x^{4} + x^{3} +8x^{2} + 14x+ 14$

Correct answer:

$x^{4} + 2x^{3} +15x^{2} + 14x+ 49$

Explanation:

$\left (x^{2} + x + 7 \right )^{2} = \left (x^{2} + x + 7 \right )\left (x^{2} + x + 7 \right )$

Vertical multiplication is perhaps the easiest way to multiply trinomials.

$x^{2} + x + 7$

$\underline{x^{2} + x + 7}$

$7x^{2} + 7x + 49$

$x ^{3 } + x^{2} + 7x$

$\underline{x ^{4 } + x^{3 } + 7x^{2} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; }$

$x^{4} + 2x^{3} +15x^{2} + 14x+ 49$

Report an Error

Example Question #17 : Simplifying Expressions

Exponentiate:

$\left ( 9R - 10\right )^{3}$

Possible Answers:

$729R^{3}-2,430R^{2} - 2,700R+1,000$

$729R^{3}-2,430R^{2} + 2,700R-1,000$

$729R^{3}-810R^{2} + 900R-1,000$

$729R^{3}-1,000$

$729R^{3}-810R^{2} - 900R+1,000$

Correct answer:

$729R^{3}-2,430R^{2} + 2,700R-1,000$

Explanation:

The difference of two terms can be cubed using the pattern

$(A-B)^{3} = A ^{3}-3A^{2}B + 3A B^{2}-B^{3}$

Where A = 9R, B = 10 :

$(A-B)^{3} = A ^{3}-3A^{2}B + 3A B^{2}-B^{3}$

$(9R-10)^{3} = (9R) ^{3}-3(9R)^{2}\cdot 10 + 3(9R) \cdot 10^{2}-10^{3}$

$(9R-10)^{3} =729R^{3}-3\cdot 81R^{2}\cdot 10 + 3(9R) \cdot 100-1,000$

$(9R-10)^{3} =729R^{3}-2,430R^{2} + 2,700R-1,000$

Report an Error

Example Question #18 : Simplifying Expressions

How many of the following are prime factors of $81y^{4}- 1$ ?

I) $9y^{2} + 1$

II) $3y^{2} + 1$

III) 3y+1

IV) 3y-1

Possible Answers:

None

One

Four

Three

Two

Correct answer:

Three

Explanation:

Factor $y^{4}- 81$ all the way to its prime factorization.

$y^{4}- 81$ can be factored as the difference of two perfect square terms as follows:

$y^{4}- 81$

$=\left ( 9y^{2} \right )^{2} - 1^{2}$

$=\left (9 y^{2} + 1 \right )\left ( 9y^{2} - 1 \right )$

$9y^{2} + 1$ is a factor, and, as the sum of squares, it is a prime. $9y^{2} - 1$ is also a factor, but it is not a prime factor - it can be factored as the difference of two perfect square terms. We continue:

$\left (9 y^{2} + 1 \right )\left ( 9y^{2} - 1 \right )$

$=\left ( 9y^{2} + 1 \right )\left [ \left (3y \right ) ^{2} - 1^{2} \right ]$

$=\left ( 9y^{2} + 1 \right )\left (3y+1 \right )\left (3 y-1\right )$

Therefore, of the given four choices, only $3y^{2} + 1$ is not a factor, so the correct response is three.

Report an Error

Example Question #4542 : Algebra 1

$\small \frac{x^2-5x-6}{x+1}$

For all values $x\neq -1$ , which of the following is equivalent to the expression above?

Possible Answers:

$\small x-3$

$\small x+6$

$\small x-2$

$\small x-6$

Correct answer:

$\small x-6$

Explanation:

First, factor the numerator. We need factors that multiply to $\small -6$ and add to $\small -5$ .

$\small 1*-6=-6\ \text{and}\ 1+(-6)=-5$

$\small x^2-5x-6=(x-6)(x+1)$

We can plug the factored terms into the original expression.

$\small \frac{x^2-5x-6}{x+1}=\frac{(x-6)(x+1)}{(x+1)}$

Note that $\small (x+1)$ appears in both the numerator and the denominator. This allows us to cancel the terms.

$\frac{(x-6)(x+1)}{(x+1)}=(x-6)$

This is our final answer.

Report an Error

Example Question #13 : Simplifying Expressions

Simplify the following expression:

3x+18y=81

Possible Answers:

2x+9y=40

x+18y=81

3x+6y=27

x+6y=27

x+6y=81

Correct answer:

x+6y=27

Explanation:

When simplifying an equation,you must find a common factor for all values in the equation, including both sides.

3,18, and, can all be divided by so divide them all at once

$\left ( \frac{3}{3}=1, \frac{18}{3}=6, \frac{81}{3}=27\right )$ .

This leaves you with

x+6y=27 .

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Tarvinder
Certified Tutor

University of Arkansas - Monticello, Bachelor of Science, Mathematics. Tulane University of Louisiana, Master of Science, Com...

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Houston, GRE Tutors in Dallas Fort Worth, Reading Tutors in Dallas Fort Worth, GRE Tutors in Denver, Computer Science Tutors in Miami, Algebra Tutors in Chicago, Biology Tutors in Atlanta, Physics Tutors in Phoenix, Computer Science Tutors in Houston, LSAT Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Atlanta, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, LSAT Courses & Classes in Denver, LSAT Courses & Classes in San Diego, SAT Courses & Classes in Miami, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Atlanta, SAT Test Prep in San Diego, GRE Test Prep in Miami, MCAT Test Prep in Miami, GRE Test Prep in San Diego, GMAT Test Prep in Seattle, GRE Test Prep in Phoenix, GMAT Test Prep in Houston, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Simplifying Expressions

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #111 : Single Variable Algebra

Example Question #12 : Simplifying Expressions

Example Question #13 : Simplifying Expressions

Example Question #271 : Sat Subject Test In Math I

Example Question #272 : Sat Subject Test In Math I

Example Question #122 : Single Variable Algebra

Example Question #17 : Simplifying Expressions

Example Question #18 : Simplifying Expressions

Example Question #4542 : Algebra 1

Example Question #13 : Simplifying Expressions

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: