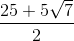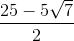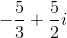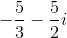We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Irrational Numbers

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 Next →

Example Question #1 : The Number System

Which of the following is not an irrational number?

Possible Answers:

$\sqrt[6]{125}$

$\sqrt[2]{125}$

$\sqrt[5]{125}$

$\sqrt[3]{125}$

$\sqrt[4]{125}$

Correct answer:

$\sqrt[3]{125}$

Explanation:

A root of an integer is one of two things, an integer or an irrational number. By testing all five on a calculator, only $\sqrt[3]{125}$ comes up an exact integer - 5. This is the correct choice.

Report an Error

Example Question #1 : Irrational Numbers

Simplify by rationalizing the denominator:

$\frac{45}{5 + \sqrt{7}}$

Possible Answers:

$\frac{ 25 + \sqrt{7} }{ 2}$

$\frac{ 25 - \sqrt{7} }{ 2}$

$\frac{ 25 + 5 \sqrt{7} }{ 2}$

$\frac{15 \sqrt{7}}{4}$

$\frac{ 25 - 5 \sqrt{7} }{ 2}$

Correct answer:

$\frac{ 25 - 5 \sqrt{7} }{ 2}$

Explanation:

Multiply the numerator and the denominator by the conjugate of the denominator, which is $5 - \sqrt{7}$ . Then take advantage of the distributive properties and the difference of squares pattern:

$\frac{45}{5 + \sqrt{7}}$

$= \frac{45\left (5 - \sqrt{7} \right )}{\left (5 + \sqrt{7} \right )\left (5 - \sqrt{7} \right )}$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 5 ^{2}- \left ( \sqrt{7} \right ) ^{2} }$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 25 -7}$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 18}$

$= \frac{5\left (5 - \sqrt{7} \right )}{ 2}$

$= \frac{ 25 - 5 \sqrt{7} }{ 2}$

Report an Error

Example Question #1 : Complex Imaginary Numbers

$\frac{-5+10i}{3+4i}=?$

Possible Answers:

$-\frac{5}{3}+\frac{5}{2}i$

$-\frac{5}{3}-\frac{5}{2}i$

1+2i

-1+2i

1-2i

Correct answer:

1+2i

Explanation:

$\frac{-5+10i}{3+4i}$

$=\frac{(-5+10i)(3-4i)}{(3+4i)(3-4i)}$

$=\frac{-15+20i+30i-40i^{2}}{9-16i^{2}}$

$=\frac{-15+50i+40}{9+16}$

$=\frac{25+50i}{25}$

=1+2i

Report an Error

Example Question #2 : Complex Imaginary Numbers

Multiply:

(7 + 3i) (1 - 2i)

Possible Answers:

7 - 5i

13 - 11i

7 - 17i

1 - 11i

13 - 17i

Correct answer:

13 - 11i

Explanation:

Use the FOIL technique:

(7 + 3i) (1 - 2i)

$= 7 \cdot 1 - 7 \cdot 2i + 3i \cdot 1 - 3i \cdot 2i$

$= 7 - 14i + 3i - 6i ^{2}$

= 7 - 14i + 3i - 6(-1)

= 7 - 14i + 3i +6

= 13 - 11i

Report an Error

Example Question #1 : Irrational Numbers

Evaluate:

$\left (2 + 3i \right )^{3}$

Possible Answers:

-4 6+ 9i

8 + 9i

8 - 27i

-62 + 63 i

-46 + 63 i

Correct answer:

-4 6+ 9i

Explanation:

We can set A = 2, B = 3i in the cube of a binomial pattern:

$\left ( A + B\right ) ^{3} = A ^{3} + 3 A^{2 }B + 3AB^{2} + B^{3}$

$= 2 ^{3} + 3 \cdot 2 ^{2 } \cdot 3i + 3 \cdot 2 \cdot (3i)^{2} + (3i)^{3}$

$= 2^{3} + 3 \cdot 2^{2} \cdot 3i + 3 \cdot 2 \cdot 3 ^{2}\cdot i^{2} + 3^{3} \cdot i^{3}$

$= 8 + 36i + 54 i^{2} + 27 i^{3}$

= 8 + 36i + 54 (-1) + 27 (-i)

= 8 + 36i - 54 - 27 i

= -46 + 9i

Report an Error

Example Question #3 : Complex Imaginary Numbers

Evaluate $\small \frac{-6+2i}{10-3i}$

Possible Answers:

$\small \frac{-54+38i}{109}$

$\small \frac{-66+2i}{109}$

$\small \small \frac{-66+2i}{91-60i}$

$\small \small \frac{-54+38i}{91-60i}$

You cannot divide by complex numbers

Correct answer:

$\small \frac{-66+2i}{109}$

Explanation:

To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, $\small 10-3i$ is our denominator, so we will multiply the expression by $\small \frac{10+3i}{10+3i}$ to obtain:

$\small \frac{-6+2i}{10-3i}\frac{10+3i}{10+3i}=\frac{-60+20i-18i+6i^2}{100-30i+30i-9i^2}$ .

We can then combine like terms and rewrite all $\small i^2$ terms as $\small -1$ . Therefore, the expression becomes:

$\small \frac{-60+2i+6i^2}{100-9i^2}=\frac{-66+2i}{109}$

Our final answer is therefore $\small \frac{-66+2i}{109}$

Report an Error

Example Question #4 : Complex Imaginary Numbers

Simplify the following product:

{} (5+3i)(-2+i)

Possible Answers:

{} -10+3i

{}-7-i

{} -13-i

{} -13+11i

Correct answer:

{} -13-i

Explanation:

Multiply these complex numbers out in the typical way:

${}(5+3i)(-2+i) = -10+5i-6i+3i^2$

and recall that i^2=-1 by definition. Then, grouping like terms we get

{} (-10-3)+(5i-6i) = -13-i

which is our final answer.

Report an Error

Example Question #5 : Complex Imaginary Numbers

Identify the real part of 1-3i

Possible Answers:

none of the above.

Correct answer:

Explanation:

A complex number in its standard form is of the form: a+bi , where stands for the real part and stands for the imaginary part. The symbol stands for $\sqrt{-1}$ .

The real part in this problem is 1.

Report an Error

Example Question #6 : Complex Imaginary Numbers

Simplify:

(4-6i)+(7+2i)

Possible Answers:

5+2i

3-4i

-3+4i

11-4i

Correct answer:

11-4i

Explanation:

To add complex numbers, find the sum of the real terms, then find the sum of the imaginary terms.

(4-6i)+(7+2i)=(4+7)+(-6+2)i=11-4i

Report an Error

Example Question #2 : Irrational Numbers

Simplify:

(5+8i)(6-2i)

Possible Answers:

7+16i

16+32i

46+38i

25+8i

Correct answer:

46+38i

Explanation:

Start by using FOIL. Which means to multiply the first terms together then the outer terms followed by the inner terms and lastly, the last terms.

(5+8i)(6-2i)=30-10i+48i-16i^2

Remember that $i=\sqrt-1$ , so i^2=-1 .

Substitute in for i^2

30-10i+48i-16i^2=30+38i-16(-1)=30+38i+16=46+38i

Report an Error

← Previous 1 2 3 Next →

View SAT Subject Test in Mathematics Level 1 Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Maggie
Certified Tutor

New York University, Bachelor of Science, Digital Communications and Multimedia.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Miami, GMAT Tutors in Phoenix, SSAT Tutors in Phoenix, Math Tutors in San Francisco-Bay Area, French Tutors in Dallas Fort Worth, Math Tutors in Phoenix, Algebra Tutors in Los Angeles, Physics Tutors in San Diego, SAT Tutors in San Diego, Math Tutors in Dallas Fort Worth

Popular Courses & Classes

ACT Courses & Classes in Los Angeles, ACT Courses & Classes in Denver, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Los Angeles, GRE Courses & Classes in Miami, ACT Courses & Classes in Chicago, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in New York City, SSAT Courses & Classes in Miami, ACT Courses & Classes in Washington DC

Popular Test Prep

ISEE Test Prep in Denver, GRE Test Prep in Miami, GRE Test Prep in Los Angeles, GRE Test Prep in Denver, LSAT Test Prep in Seattle, GRE Test Prep in San Diego, ACT Test Prep in Boston, ACT Test Prep in Washington DC, ACT Test Prep in Houston, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Irrational Numbers

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : The Number System

Example Question #1 : Irrational Numbers

Example Question #1 : Complex Imaginary Numbers

Example Question #2 : Complex Imaginary Numbers

Example Question #1 : Irrational Numbers

Example Question #3 : Complex Imaginary Numbers

Example Question #4 : Complex Imaginary Numbers

Example Question #5 : Complex Imaginary Numbers

Example Question #6 : Complex Imaginary Numbers

Example Question #2 : Irrational Numbers

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: