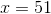All SAT II Math I Resources
Example Questions
Example Question #61 : 2 Dimensional Geometry
Regular Pentagon 
Give the length of diagonal 
The perimeter of the regular pentagon is 80, so each side measures one fifth of this, or 16. Also, each interior angle of a regular pentagon measures 
The pentagon, along with diagonal 

A triangle 



where 



Setting 


Taking the square root of both sides:

the correct choice.
Example Question #441 : Advanced Geometry





5
12
30
24
15
24
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,
Example Question #1 : Finding Angles
What angle do the minute and hour hands of a clock form at 4:45?
There are twelve numbers on a clock; from one to the next, a hand rotates 


Example Question #1 : Finding Angles
What angle do the minute and hour hands of a clock form at 8:50?
There are twelve numbers on a clock; from one to the next, a hand rotates 



Example Question #62 : 2 Dimensional Geometry

Note: Figure NOT drawn to scale.
The above hexagon is regular. What is 
Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

The four angles of the quadrilateral are 


Example Question #61 : Geometry
Can a triangle have a set of angles that are 

Yes
No
No
A triangle's angles must add up to 
The angles given add up to 181,

That means that this cannot be an actual triangle.
Example Question #5 : Finding Angles
If two angles of a triangle are 

Step 1: Recall the sum of the angles of a triangle...
The sum of the internal angles of a triangle is 
Step 2: To find the missing angle, subtract the given angles from 
Example Question #1 : Analyzing Figures
The sides of a triangle have lengths 6 yards, 18 feet, and 216 inches. Which of the following is true about this triangle?
This triangle is acute and isosceles, but not equilateral.
This triangle is acute and scalene.
The triangle is acute and equilateral.
This triangle is right and isosceles, but not equilateral.
This triangle is right and scalene.
The triangle is acute and equilateral.
One yard is equal to 3 feet; it is also equal to 36 inches. Therefore:
18 feet is equal to 
and
216 feet is equal to 
The three sides are congruent, making the triangle equilateral - and all equilateral triangles are acute.
Example Question #63 : Geometry

Figures not drawn to scale
The triangles above are similar. Given the measurements above, what is the length of side c?






You can find the length of c by first finding the length of the hypotenuse of the larger similar triangle and then setting up a ratio to find the hypotenuse of the smaller similar triangle.
You also could have found 10 by recognizing this triangle is a form of a 3-4-5 triangle.
The hypotenuse of the bigger triangle is 10 inches.
Now that we know the length of the hypotenuse for the larger triangle, we can set up a ratio equation to find the hypotenuse of the smaller triangle.

Example Question #2 : Analyzing Figures

If line 2 and line 3 eventually intersect when extended to the left which of the following could be true?
I and III
I and II
I, II, and III
I only
Cannot be determined
I only
Read the question carefully and notice that the image is deceptive: these lines are not parallel. So we cannot apply any of our rules about parallel lines. So we cannot infer II or III, those are only true if the lines are parallel. If we sketch line 2 and line 3 meeting we will form a triangle and it is possible to make a = e. One such solution is to make a and e 60 degrees.
All SAT II Math I Resources