All SAT II Math I Resources
Example Questions
Example Question #1 : Diameter, Radius, And Circumference

Find the diameter, circumference and area of the circle above.
Diameter= 6ft
Circumference=37.68 ft
Area= 28.27 ft2
Diameter= 6 ft
Circumference= 19 ft
Area= 30 ft2
Diameter= 6 ft
Circumference=18.84 ft
Area= 28.27 ft2
Diameter= 9ft
Circumference=37.68 ft
Area= 28 ft2
Diameter= 3ft
Circumference=37.68 ft
Area= 28.7 ft2
Diameter= 6 ft
Circumference=18.84 ft
Area= 28.27 ft2
To find the diameter, you must know that radius is half the diameter (or the diameter is 2 times the radius.
The diameter is 6ft.
To find the circumference, you must multiply the diameter (6ft) by pi.
The circumference is 18.84 ft.
To find the surface area, you must aquare the radius (3ft) and multiply by pi.
The surface area is 28.27 ft2.
The diameter is 6ft, the circumference is 18.84 ft, and the surface area is 28.27 ft2.
Example Question #31 : Geometry
A circle has a diameter of 10cm. What is the circumference?
The circumference of a circle is given by the equation:
The radius is half the diameter, in this case half of 10cm is 5cm
Plug in 5cm for r
Simplify to get the final answer
Example Question #1 : Diameter, Radius, And Circumference
If the diameter of a circle is 
Step 1: Recall the formula for an area of a circle...

Step 2: Given the diameter, find the radius..
We know that the diameter is twice the length of the radius...
Plug in 

Divide by 2:
Step 3: Now that we know the radius, plug the radius into the area formula..
Simplify:
Example Question #34 : Geometry
Determine the circumference of the circle with an area of 
Write the formula for the area of a circle.
Substitute the area.
Square root both sides to solve for radius.
Write the formula for circumference.
Substitute the radius.
The answer is:
Example Question #2 : Diameter, Radius, And Circumference
Find the diameter of a circle if the circumference is 
Write the formula for the circumference of the circle.
Substitute the circumference into the equation.
Divide by pi on both sides to get the diameter.
The answer is:
Example Question #36 : Geometry
Find the area of a circle if the circumference is 
Write the formula for the circumference of a circle.
Substitute the circumference.
Divide by 

The radius is:
Write the formula for the area of the circle.
Substitute the radius.
The answer is:
Example Question #31 : 2 Dimensional Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate the length of the hypotenuse of the blue triangle.
The inscribed rectangle is a 20 by 20 square. Since opposite sides of the square are parallel, the corresponding angles of the two smaller right triangles are congruent; therefore, the two triangles are similar and, by definition, their sides are in proportion.
The small top triangle has legs 10 and 20. Therefore, the length of its hypotenuse can be determined using the Pythagorean Theorem:
The small top triangle has short leg 10 and hypotenuse 


Example Question #1 : Finding Sides

Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.

Evaluate 
By the Law of Sines,
Substitute 

Example Question #31 : 2 Dimensional Geometry

Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate 
By the Law of Cosines,
Substitute 
Example Question #2 : Finding Sides

The above figure is a regular pentagon. Evaluate 
Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures
The length of the third side can be found by applying the Law of Cosines:
where 
All SAT II Math I Resources




















































































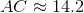
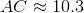












![m = \left [\frac{180(5-2)}{5} \right ] ^{\circ }= 108^{\circ }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/216649/gif.latex)









