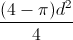Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #62 : Circles

A circle with diameter of length $\dpi{100} d$ is inscribed in a square. Which of the following is equivalent to the area inside of the square, but outside of the circle?

Possible Answers:

$\frac{(4-\pi)d^2}{4}$

$d^{2}-4$

$\pi d^{2}+2$

$\frac{(\pi - 1)d^2}{4}$

$(\pi - 1)d^2$

Correct answer:

$\frac{(4-\pi)d^2}{4}$

Explanation:

In order to find the area that is inside the square but outside the circle, we will need to subtract the area of the circle from the area of the square. The area of a circle is equal to $\pi r^2$ . However, since we are given the length of the diameter, we will need to solve for the radius in terms of the diameter. Because the diameter of a circle is twice the length of its radius, we can write the following equation and solve for $\dpi{100} r$ :

$\dpi{100} d=2r$

Divide both sides by 2.

$r = \frac{d}{2}$

We will now substitute this into the formula for the area of the circle.

area of circle = $\pi r^2 = \pi(\frac{d}{2})^2=\pi \frac{d}{2}\cdot \frac{d}{2}= \frac{\pi d^2}{4}$

We next will need to find the area of the square. Because the circle is inscribed in the square, the diameter of the circle is equal to the length of the circle's side. In other words, the square has side lengths equal to d. The area of any square is equal to the square of its side length. Therefore, the area of the square is $d^{2}$ .

area of square = $d^{2}$

Lastly, we will subtract the area of the circle from the area of the square.

difference in areas = $d^2 - \frac{\pi d^2}{4}$

We will rewrite $d^{2}$ so that its denominator is 4.

difference in areas = $\frac{4d^2}{4}-\frac{\pi d^2}{4}=\frac{(4-\pi)d^2}{4}$

The answer is $\frac{(4-\pi)d^2}{4}$ .

Report an Error

Example Question #21 : Radius

An original circle has an area of $16\pi$ . If the radius is increased by a factor of 3, what is the ratio of the new area to the old area?

Possible Answers:

$7:1$

$10:1$

$8:1$

$3:1$

$9:1$

Correct answer:

$9:1$

Explanation:

The formula for the area of a circle is $\pi r^{2}$ . If we increase $r$ by a factor of 3, we will increase the area by a factor of 9.

Report an Error

Example Question #14 : Radius

A square has an area of $36\ in^{2}$ . If the side of the the square is the same as the diameter of a circle, what is the area of the circle?

Possible Answers:

$27\pi \ in^{2}$

$36\pi \ in^{2}$

$12\pi \ in^{2}$

$9\pi \ in^{2}$

$18\pi \ in^{2}$

Correct answer:

$9\pi \ in^{2}$

Explanation:

The area of a square is given by $A = s^{2}$ so we know that the side of the square is 6 in. If a circle has a diameter of 6 in, then the radius is 3 in. So the area of the circle is $A = \pi r^{2}$ or $9\pi \ in^{2}$ .

Report an Error

Example Question #71 : Circles

Mary has a decorative plate with a diameter of ten inches. She places the plate on a rectangular placemat with a length of 18 inches and a width of 12 inches. How much of the placemat is visible?

Possible Answers:

$191\pi\hspace{1 mm}inches^2$

$216\hspace{1 mm}inches^2$

$216-25\pi\hspace{1 mm}inches^2$

$25\pi\hspace{1 mm}inches^2$

$216\pi\hspace{1 mm}inches^2$

Correct answer:

$216-25\pi\hspace{1 mm}inches^2$

Explanation:

First we will calculate the total area of the placemat:

$A=l\times w= 18\times 12= 216\hspace{1 mm}inches^2$

Next we will calculate the area of the circular place

$A=\pi r^2$

And

$d=2r=10$

$r=5\hspace{1 mm}inches$

$A=\pi r^2=\pi (5^2)=25\pi\hspace{1 mm}inches^2$

We will subtract the area of the plate from the total area

$216-25\pi\hspace{1 mm}inches^2$

Report an Error

Example Question #22 : Radius

The picture above contains both a circle with diameter 4, and a rectangle with length 8 and width 5. Find the area of the shaded region. Round your answer to the nearest integer

Possible Answers:

Correct answer:

Explanation:

First, recall that the diameter of a circle is twice the value of the radius. Therefore a circle with diameter 4 has a radius of 2. Next recall that the area of a circle with radius r=2 is:

$\pi r^2 = \pi(2)^2 = 4 \pi$

The area of the rectangle is the length times the width:

$L \times W = 8 \times 5 = 40$

The area of the shaded region is the difference between the 2 areas:

$40 - 4 \pi \approx 40-4(3.14) = 27.44$

The nearest integer is 27.

Report an Error

Example Question #21 : Radius

Allen was running around the park when he lost his keys. He was running around aimlessly for the past 30 minutes. When he checked 10 minutes ago, he still had his keys. Allen guesses that he has been running at about 3m/s.

If Allen can check 1 square kilometer per hour, what is the longest it will take him to find his keys?

Possible Answers:

$\sim 81\ hours$

$\sim 10\ hours$

$\sim 100\ hours$

$\sim 1,000\ hours$

$\sim 3\ hours$

Correct answer:

$\sim 10\ hours$

Explanation:

Allen has been running for 10 minutes since he lost his keys at 3m/s. This gives us a maximum distance of 3*600=1800m from his current location. If we move 1800m in all directions, this gives us a circle with radius of 1800m. The area of this circle is

$1800^2\pi \approx 10,178,760m^2$

Our answer, however, is asked for in kilometers. 1800m=1.8km, so our actual area will be $\frac{10,178,760}{1,000,000} = 10.2$ square kilometers. Since he can search 1 per hour, it will take him at most 10.2 hours to find his keys.

Report an Error

Example Question #321 : Plane Geometry

A 12x16 rectangle is inscribed in a circle. What is the area of the circle?

Possible Answers:

10π

90π

50π

120π

100π

Correct answer:

100π

Explanation:

Explanation: Visualizing the rectangle inside the circle (corners touching the circumference of the circle and the center of the rectangle is the center of the circle) you will see that the rectangle can be divided into 8 congruent right triangles, with the hypotenuse as the radius of the circle. Calculating the radius you divide each side of the rectangle by two for the sides of each right triangle (giving 6 and 8). The hypotenuse (by pythagorean theorem or just knowing right triangle sets) the hypotenuse is give as 10. Area of a circle is given by πr². 10² is 100, so 100π is the area.

Report an Error

Example Question #322 : Plane Geometry

A circle is inscribed in a square whose side is 6 in. What is the difference in area between the square and the circle, rounded to the nearest square inch?

Possible Answers:

$12\ in^{2}$

$8\ in^{2}$

$4\ in^{2}$

$11\ in^{2}$

$14\ in^{2}$

Correct answer:

$8\ in^{2}$

Explanation:

The circle is inscribed in a square when it is drawn within the square so as to touch in as many places as possible. This means that the side of the square is the same as the diameter of the circle.

Let $\pi =3.14$

$A_{square}= s^{2} = (6)^{2} = 36 in^{2}$

$A_{circle}= \pi r^{2}=3.14\cdot3^{2}=3.14\cdot9=28.26 in^{2}$

So the approximate difference is in area $8\ \textup{in}^{2}$

Report an Error

Example Question #321 : Plane Geometry

Two equal circles are cut out of a rectangular sheet of paper with the dimensions 10 by 20. The circles were made to have the greatest possible diameter. What is the approximate area of the paper after the two circles have been cut out?

Figure_2

Possible Answers:

Correct answer:

Explanation:

The length of 20 represents the diameters of both circles. Each circle has a diameter of 10 and since radius is half of the diameter, each circle has a radius of 5. The area of a circle is A = πr² . The area of one circle is 25π. The area of both circles is 50π. The area of the rectangle is (10)(20) = 200. 200 - 50π gives you the area of the paper after the two circles have been cut out. π is about 3.14, so 200 – 50(3.14) = 43.

Report an Error

Example Question #101 : Geometry

Screen_shot_2013-03-18_at_10.29.01_pm

Kate has a ring-shaped lawn which has an inner radius of 10 feet and an outer radius 25 feet. What is the area of her lawn?

Possible Answers:

325π ft²

525π ft²

175π ft²

275π ft²

125π ft²

Correct answer:

525π ft²

Explanation:

The area of an annulus is

$\pi (R^{2}-r^{2})$

where is the radius of the larger circle, and is the radius of the smaller circle.

$\pi (25^{2}-10^{2})$

$\pi (625-100)$

$525\pi$

Report an Error

View PSAT Mathematics Tutors

Justin
Certified Tutor

University of Rhode Island, Master of Science, Industrial Engineering.

View PSAT Mathematics Tutors

Evgenii
Certified Tutor

View PSAT Mathematics Tutors

Seung Soo
Certified Tutor

College of William and Mary, Current Undergrad Student, Neuroscience.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Seattle, Computer Science Tutors in Boston, French Tutors in San Francisco-Bay Area, SSAT Tutors in Philadelphia, Chemistry Tutors in Philadelphia, Biology Tutors in Los Angeles, Spanish Tutors in Chicago, ACT Tutors in Atlanta, Physics Tutors in Denver, Chemistry Tutors in Washington DC

Popular Courses & Classes

ACT Courses & Classes in Los Angeles, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Boston, LSAT Courses & Classes in Seattle, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Atlanta, LSAT Courses & Classes in Houston

Popular Test Prep

ISEE Test Prep in Boston, SSAT Test Prep in Los Angeles, SAT Test Prep in Houston, ACT Test Prep in Houston, ISEE Test Prep in Chicago, SSAT Test Prep in Seattle, SSAT Test Prep in Houston, ISEE Test Prep in Philadelphia, LSAT Test Prep in Philadelphia, GMAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #62 : Circles

Example Question #21 : Radius

Example Question #14 : Radius

Example Question #71 : Circles

Example Question #22 : Radius

Example Question #21 : Radius

Example Question #321 : Plane Geometry

Example Question #322 : Plane Geometry

Example Question #321 : Plane Geometry

Example Question #101 : Geometry

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: