All PSAT Math Resources
Example Questions
Example Question #12 : Basic Operations
What number replaces the circle in the following sequence?
The sequence is formed by starting with 1 and adding successive powers of 5. The numbers are obtained as follows:

Example Question #1 : How To Add Integers
Suppose you know the values of the variables in the expression
and you wish to evaluate it.
Which operation do you execute last?
Division
Addition
Multiplication
Subtraction
Squaring
Addition
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
Example Question #1882 : Psat Mathematics
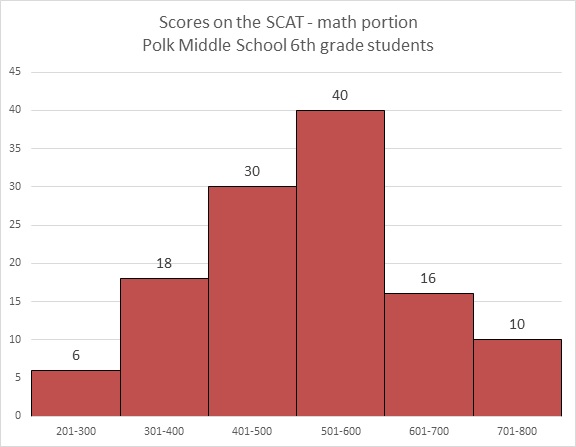
Refer to the above graph. Francie, a sixth grader at Polk, scored a 372 on the math portion of the SCAT. Which of the following could have been her rank among the students?
By scoring a 372, Francie was outcored by all of the students who finished in the 401-800 ranges, which add up to:

She was outscored by at most an additional 17 students (the other 17 in the 301-400 range), for a total of at most

Francie finished between 97th and 114th place, making 100th place the only possible choice.
Example Question #1 : How To Find The Greatest Or Least Number Of Combinations
Mark has 5 pants and 7 shirts in his closet. He wants to wear a different pant/shirt combination each day without buying new clothes for as long as he can. How many weeks can he do this for?
6
7
4
5
8
5
The fundamental counting principle says that if you want to determine the number of ways that two independent events can happen, multiply the number of ways each event can happen together. In this case, there are 5 * 7, or 35 unique combinations of pants & shirts Mark can wear. If he wears one combination each day, he can last 35 days, or 5 weeks, without buying new clothes.
Example Question #2 : Permutation / Combination
Twenty students enter a contest at school. The contest offers a first, second, and third prize. How many different combinations of 1st, 2nd, and 3rd place winners can there be?
6840
20
4620
400
8000
6840
This is a permutation problem, because we are looking for the number of groups of winners. Consider the three positions, and how many choices there are for each position: There are 20 choices for 1st place, 19 for 2nd place, and 18 for 3rd place.
20, 19, 18
Multiply to get 6840.
Example Question #1 : How To Find The Greatest Or Least Number Of Combinations
A baker has four different types of frosting, three different kinds of sprinkles, and 8 different cookie cutters. How many different cookie combinations can the baker create if each cookie has one type of frosting and one type of sprinkle?
15
96
48
24
96
Since this a combination problem and we want to know how many different ways the cookies can be created we can solve this using the Fundamental counting principle. 4 x 3 x 8 = 96
Multiplying each of the possible choices together.
Example Question #2 : Permutation / Combination
If a series of license plates is to be produced that all have the same pattern of three letters followed by three numbers, roughly how many alphanumeric combinations are possible?
180 million
18 thousand
18 million
1 thousand
11 million
18 million
The total number of possible combinations of a series of items is the product of the total possibility for each of the items. Thus, for the letters, there are 26 possibilities for each of the 3 slots, and for the numbers, there are 10 possibilities for each of the 3 slots. The total number of combinations is then: 26 x 26 x 26 x 10 x 10 x 10 = 17,576,000 ≈ 18 million.
Example Question #1 : Permutation / Combination
If there are 8 points in a plane, and no 3 of the points lie along the same line, how many unique lines can be drawn between pairs of these 8 points?
27
30
28
29
28
The formula for the number of lines determined by n points, no three of which are “collinear” (on the same line), is n(n-1)/2. To find the number of lines determined by 8 points, we use 8 in the formula to find 8(8-1)/2=8(7)/2=56/2=28. (The formula is derived from two facts: the fact that each point forms a line with each other point, hence n(n-1), and the fact that this relationship is symmetric (i.e. if a forms a line with b, then b forms a line with a), hence dividing by 2.)
Example Question #3 : Permutation / Combination
8 people locked in a room take turns holding hands with each person only once. How many hand holdings take place?
28
21
24
15
28
The first person holds 7 hands. The second holds six by virtue of already having help the first person’s hand. This continues until through all 8 people. 7+6+5+4+3+2+1=28.
Example Question #1 : Permutation / Combination
At an ice cream store, there are 5 flavors of ice cream: strawberry, vanilla, chocolate, mint, and banana. How many different 3-flavor ice cream cones can be made?
30
5
60
20
10
10
There are 5x4x3 ways to arrange 5 flavors in 3 ways. However, in this case, the order of the flavors does not matter (e.g., a cone with strawberry, mint, and banana is the same as a cone with mint, banana, and strawberry). So we have to divide 5x4x3 by the number of ways we can arrange 3 different things which is 3x2x1. So (5x4x3)/(3x2x1) is 10.
One can also use the combination formula for this problem: nCr = n! / (n-r)! r!
Therefore: 5C3 = 5! / 3! 2!
= 10
(Note: an example of a counting problem in which order would matter is a lock or passcode situation. The permutation 3-5-7 for a three number lock or passcode is a distinct outcome from 5-7-3, and thus both must be counted.)
All PSAT Math Resources