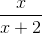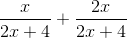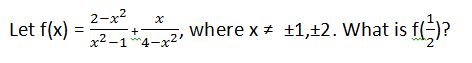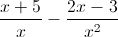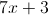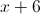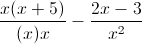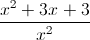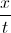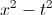All PSAT Math Resources
Example Questions
Example Question #1 : Rational Expressions
Simplify the expression.
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
This is the most simplified version of the rational expression.
Example Question #1 : How To Evaluate Rational Expressions
If √(ab) = 8, and a2 = b, what is a?
2
4
64
10
16
4
If we plug in a2 for b in the radical expression, we get √(a3) = 8. This can be rewritten as a3/2 = 8. Thus, loga 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
Example Question #2 : How To Evaluate Rational Expressions
–37/15
9/5
–9/5
–11/5
37/15
–11/5
Example Question #4 : Rational Expressions
Simplify.
Determine an LCD (Least Common Denominator) between 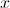
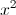
LCD =
Multiply the top and bottom of the first rational expression by 

Distribute the 

Now you can subtract because both rational expressions have the same denominators.
Final Answer.
Example Question #1 : How To Divide Rational Expressions
Which of the following is equivalent to 
We will need to simplify the expression . We can think of this as a large fraction with a numerator of


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

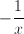


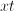
In order to convert the fraction 
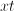

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction . We will now rewrite the numerator:
=
To simplify this further, we can think of 


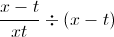
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
Example Question #4 : Rational Expressions
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
4/(x – 2)2
(4x2 + 8x)/(x4 + 8x)
x/(x + 2)
4/(x + 2)2
x/(x – 2)2
4/(x – 2)2
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Example Question #4 : Rational Expressions
what is 6/8 X 20/3
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
Example Question #1 : How To Add Exponents
If a2 = 35 and b2 = 52 then a4 + b6 = ?
150,000
522
3929
140,608
141,833
141,833
a4 = a2 * a2 and b6= b2 * b2 * b2
Therefore a4 + b6 = 35 * 35 + 52 * 52 * 52 = 1,225 + 140,608 = 141,833
Example Question #2 : Exponential Operations
If 

Since we have two 

For 
So we have 
Or
Divide this by 
Thus 
*Hint: If you are really unsure, you could have plugged in the numbers and found that the first choice worked in the equation.
Example Question #3 : Exponential Operations
Solve for x.
23 + 2x+1 = 72
4
3
6
7
5
5
The answer is 5.
8 + 2x+1 = 72
2x+1 = 64
2x+1 = 26
x + 1 = 6
x = 5
Certified Tutor
All PSAT Math Resources