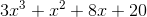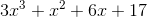The polynomial has one term, so its degree is the sum of the exponents of the variables:

$\displaystyle 12+14 + 16+18 =60$

The degree of a polynomial in more than one variable is the greatest degree of any of the terms; the degree of a term is the sum of the exponents. The degrees of the terms in the given polynomial are:

$\displaystyle 50 + 30 = 80$

$\displaystyle 70 + 25= 95$

$\displaystyle 45+45 = 90$

$\displaystyle 30 + 70 = 100$

The degree of the polynomial is the greatest of these degrees, 100.

The degree of a polynomial in one variable is the greatest exponent of any of the powers of the variable. The terms have as their exponents, in order, 44, 20, 10, and 100; the greatest of these is 100, which is the degree.

The degree of a polynomial in one variable is the greatest exponent of any of the powers of the variable. The terms have as their exponents, in order, 10, 20, 30, and 40; 40 is the greatest of them and is the degree of the polynomial.

The degree of a polynomial is the highest degree of any term; the degree of a term is the exponent of its variable or the sum of the exponents of its variables, with unwritten exponents being equal to 1. For each term in a polynomial, write the exponent or add the exponents; the greatest number is its degree. We do this with all four choices:

$\displaystyle \underline{6x^{3}y^{2} + 4 xy^{3} - 100}$:

$\displaystyle 6x^{3}y^{2}: 3 + 2 = 5$

$\displaystyle 4 xy^{3}: 1 + 3 = 4$

$\displaystyle 100:$ A constant term has degree 0.

The degree of this polynomial is 5.

$\displaystyle \underline{7xy^{4} - 4x^{2}+ y^{3}}$

$\displaystyle 7xy^{4} : 1 + 4 = 5$

$\displaystyle 4x^{2} : 2$

$\displaystyle y^{3}: 3$

The degree of this polynomial is 5.

$\displaystyle \underline{8x ^{4}y - 4 y^{2} + 9x^{3}y}$

$\displaystyle 8x ^{4}y: 4 + 1= 5$

$\displaystyle 4 y^{2} : 2$

$\displaystyle 9x^{3}y: 3 + 1= 4$

The degree of this polynomial is 5.

$\displaystyle \underline{-5 x^{2}y^{2}+ 7x^{3}y^{2}+ 8x}$

$\displaystyle -5 x^{2}y^{2} : 2 + 2 = 4$

$\displaystyle 7x^{3}y^{2} : 3 + 2 = 5$

$\displaystyle 8x: 1$

The degree of this polynomial is 5.

All four polynomials have the same degree.

The degree of a monomial term is the sum of the exponents of its variables, with the default being 1.

For each monomial, this sum - and the degree - is as follows:

$\displaystyle 444x^{999}yz$: $\displaystyle 999 + 1 + 1 = 1,001$

$\displaystyle 333x^{999}y^{999}z^{999}$: $\displaystyle 999+999+999 = 2,997$

$\displaystyle 999x^{4}y^{5}z^{6}$: $\displaystyle 4+5+6 = 15$ (note - 999 is the coefficient)

$\displaystyle 100x^{333}y^{333}z^{333}$: $\displaystyle 333+333+333 = 999$

$\displaystyle 100x^{333}y^{333}z^{333}$ is the correct choice.

The degree of the polynomial is the largest degree of any one of it's individual terms.

$\displaystyle \small - x^{2}+3x - 2x^{5} - x^{3} +4$

The degree of $\displaystyle \small -x^2$ is $\displaystyle \small 2$

The degree of  $\displaystyle \small 3x$ is $\displaystyle \small 1$

The degree of $\displaystyle \small -2x^5$ is $\displaystyle \small 5$

The degree of $\displaystyle \small -x^3$ is $\displaystyle \small 3$

The degree of  $\displaystyle \small 4$ is $\displaystyle \small 0$

$\displaystyle \small 5$ is the largest degree of any one of the terms of the polynomial, and so the degree of the polynomial is $\displaystyle \small 5$.

We can add together each of the terms of the polynomial which have the same degree for our variable. $\displaystyle (3x^{3}) + (x^{2}) + (5x+3x) + (12+8) = 3x^{3}+x^{2}+8x+20$

Step 1: Distribute the negative to the second polynomial:

$\displaystyle (x^4+7x^2-5x+4)-(-4x^4+5x^3-x^2+3)$

$\displaystyle x^4+7x^2-5x+4+4x^2-5x^3+x^2-3$

Step 2: Combine like terms:

$\displaystyle x^4+4x^4-5x^3+7x^2+x^2-5x+4-3$

$\displaystyle 5x^4-5x^3+8x^2-5x+1$

$\displaystyle (FG)(x) = F(x)G(x)$ so we multiply the two function to get the answer.  We use $\displaystyle x^{m}x^{n} = x^{m+n}$