PSAT Math : How to graph an inequality with a number line
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1 : How To Graph An Inequality With A Number Line
What property of arithmetic is demonstrated here?
If and , then .
Inverse
Symmetric
Transitive
Commutative
Associative
Transitive
The symbols express the idea that if a number is less than a second number, which is less than a third, then the first number is less than the third. This is the transitive property of inequality.
Example Question #1 : How To Graph An Inequality With A Number Line
On a real number line, x1 = -4 and x2 = 14. What is the distance between these two points?
4
-18
10
18
18
The distance between two points is always positive. We calculate lx2 - x1l, which will give us the distance between the points.
|14- (-4)| = |14+4| = |18| = 18
Example Question #1 : How To Graph An Inequality With A Number Line
Which of the following is a graph for the values of defined by the inequality stated above?
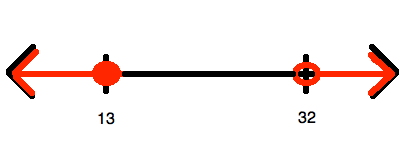
To begin, you must simplify so that you "isolate" , (i.e. at least eliminate any coefficients from it). To do this, divide all of the members of the inequality by :
Now, this inequality represents all of the numbers between 13 and 32. However, it does include (hence, getting a closed circle for that value) and does not include (hence, getting an open circle for that value). Therefore, it looks like:
Example Question #2 : How To Graph An Inequality With A Number Line
Which of the following inequalities is represented by the number line shown above?
Since the inequality represents one range of values between two end points (both of which are included, given the sign being "less than or equal"), you know that whatever you answer, it must be convertible to the form:
Now, you know that it is impossible to get this out of the choices that have no absolute values involved in them. Therefore, the only options that make sense are the two having absolute values; however, here you should choose only the ones that have a , for only that will yield a range like this. Thus, we can try both of our options.
The wrong answer is simplified in this manner:
And you can stop right here, for you know you will never have for the left terminus.
The other option is simplified in this manner:
This is just what you need!
Example Question #4 : How To Graph An Inequality With A Number Line
Which of the following is a graph for the values of defined by the inequality stated above?
Begin by solving for :
Now, this is represented by drawing an open circle at 6 and graphing upward to infinity:
Certified Tutor
All PSAT Math Resources
