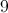Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : How to find the length of the diagonal of a hexagon

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Hexagons

How many diagonals are there in a regular hexagon?

Possible Answers:

Correct answer:

Explanation:

A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:

$\frac{n\cdot (n-3)}{2}$

where $n=\#\ of\ sides$ .

Report an Error

Example Question #1 : Hexagons

How many diagonals are there in a regular hexagon?

Possible Answers:

Correct answer:

Explanation:

A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:

$\frac{n\cdot (n-3)}{2}$

where n = the number of sides in the polygon.

Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

Regular Hexagon ABCDEF has a diagonal $\overline{AE}$ with length 1.

Give the length of diagonal $\overline{A D}$ .

Possible Answers:

$\sqrt{ 2}$

$\sqrt{3}$

$\frac{3\sqrt{2}}{2}$

$\frac{2\sqrt{3}}{3}$

Correct answer:

$\frac{2\sqrt{3}}{3}$

Explanation:

The key is to examine $\Delta AED$ in thie figure below:

Hexagon_50

Each interior angle of a regular hexagon, including $\angle F$ , measures $120^{\circ }$ , so it can be easily deduced by way of the Isosceles Triangle Theorem that $m \angle FEA = 30^{\circ }$ . $m \angle FED = 120^{\circ }$ , so by angle addition,

$m \angle AED = 90^{\circ }$ .

Also, by symmetry,

$m \angle EDA = \frac{1}{2} \cdot 120^{\circ } = 60^{\circ }$ ,

so $m \angle EAD= 30^{\circ }$ ,

and $\Delta AED$ is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle whose long leg $\overline{AE}$ has length AE= 1 .

By the $30^{\circ}-60^{\circ}-90^{\circ}$ Theorem, $\overline{AD}$ , which is the hypotenuse of $\Delta AED$ , has length $\frac{2\sqrt{3}}{3}$ times that of the long leg, so $AD =\frac{2\sqrt{3}}{3}$ .

Report an Error

Example Question #251 : Plane Geometry

Regular Hexagon ABCDEF has a diagonal $\overline{AD}$ with length 1.

Give the length of diagonal $\overline{A E}$ .

Possible Answers:

$\frac{\sqrt{3}}{3}$

$\frac{\sqrt{2}}{2}$

$\frac{2}{3}$

$\frac{\sqrt{3}}{2}$

$\frac{3\sqrt{2}}{4}$

Correct answer:

$\frac{\sqrt{3}}{2}$

Explanation:

The key is to examine $\Delta AED$ in thie figure below:

Hexagon_50

$m \angle AED = 90^{\circ }$ .

Also, by symmetry,

$m \angle EDA = \frac{1}{2} \cdot 120^{\circ } = 60^{\circ }$ ,

so $m \angle EAD= 30^{\circ }$ ,

and $\Delta AED$ is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle whose hypotenuse $\overline{AD}$ has length AD = 1 .

By the $30^{\circ}-60^{\circ}-90^{\circ}$ Theorem, the long leg $\overline{AE}$ of $\Delta AED$ has length $\frac{\sqrt{3}}{2}$ times that of hypotenuse $\overline{AD}$ , so $AE = \frac{\sqrt{3}}{2}$ .

Report an Error

Example Question #3 : How To Find The Length Of The Diagonal Of A Hexagon

Regular hexagon ABCDEF has side length of 1.

Give the length of diagonal $\overline{A D}$ .

Possible Answers:

$2\sqrt{2}$

$\sqrt{2}$

$2\sqrt{3}$

$\sqrt{3}$

Correct answer:

Explanation:

The key is to examine $\Delta AED$ in thie figure below:

Hexagon_50

Each interior angle of a regular hexagon, including $\angle F$ , measures $120^{\circ }$ , so it can be easily deduced by way of the Isosceles Triangle Theorem that $m \angle FEA = 30^{\circ }$ . To find $m \angle AED$ we can subtract $m \angle FEA = 30^{\circ }$ from $m \angle FED = 120^{\circ }$ . Thus resulting in:

$m \angle AED = 90^{\circ }$

Also, by symmetry,

$m \angle EDA = \frac{1}{2} \cdot 120^{\circ } = 60^{\circ }$ ,

so $m \angle EAD= 30^{\circ }$ .

Therefore, $\Delta AED$ is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle whose short leg $\overline{ED}$ has length ED = 1 .

The hypotenuse $\overline{AD}$ of this $30^{\circ}-60^{\circ}-90^{\circ}$ triangle measures twice the length of short leg $\overline{ED}$ , so AD = 2 .

Report an Error

Example Question #4 : How To Find The Length Of The Diagonal Of A Hexagon

Regular hexagon ABCDEF has side length 1.

Give the length of diagonal $\overline{A E}$ .

Possible Answers:

$\frac{\sqrt{2}}{2}$

$\frac{\sqrt{3}}{2}$

$\frac{3}{2}$

$\sqrt{2}$

$\sqrt{3}$

Correct answer:

$\sqrt{3}$

Explanation:

The key is to examine $\Delta AED$ in thie figure below:

Hexagon_50

Each interior angle of a regular hexagon, including $\angle F$ , measures $120^{\circ }$ , so it can be easily deduced by way of the Isosceles Triangle Theorem that $m \angle FEA = 30^{\circ }$ . To find $m \angle AED$ we subtract $m \angle FEA = 30^{\circ }$ from $m \angle FED = 120^{\circ }$ . Thus resullting in $m \angle AED=90^{\circ}$

Also, by symmetry,

$m \angle EDA = \frac{1}{2} \cdot 120^{\circ } = 60^{\circ }$ ,

so $m \angle EAD= 30^{\circ }$ ,

and $\Delta AED$ is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle whose short leg $\overline{ED}$ has length ED = 1 .

The long leg $\overline{AE}$ of this $30^{\circ}-60^{\circ}-90^{\circ}$ triangle measures $\sqrt{3}$ times the length of short leg $\overline{ED}$ , so $AE= \sqrt{3}$ .

Report an Error

View PSAT Mathematics Tutors

Deneka
Certified Tutor

College of Southern Maryland, Associate in Arts, Early Childhood Special Education.

View PSAT Mathematics Tutors

Don
Certified Tutor

Fort Lewis College, Bachelors, Mathematics, Geology. Virginia Polytechnic Institute and State University, PHD, Geosciences.

View PSAT Mathematics Tutors

Shakeel
Certified Tutor

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in San Francisco-Bay Area, Chemistry Tutors in San Francisco-Bay Area, Spanish Tutors in Atlanta, SSAT Tutors in Houston, SAT Tutors in Boston, Math Tutors in San Diego, ACT Tutors in Washington DC, GMAT Tutors in Phoenix, Computer Science Tutors in San Francisco-Bay Area, Reading Tutors in San Diego

Popular Courses & Classes

GRE Courses & Classes in Chicago, SAT Courses & Classes in Denver, LSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Houston, MCAT Courses & Classes in Denver, ACT Courses & Classes in Philadelphia, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Chicago, ISEE Test Prep in San Diego, LSAT Test Prep in Chicago, SSAT Test Prep in Denver, GRE Test Prep in Denver, LSAT Test Prep in Los Angeles, LSAT Test Prep in Denver, SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Philadelphia, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : How to find the length of the diagonal of a hexagon

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : Hexagons

Example Question #1 : Hexagons

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

Example Question #251 : Plane Geometry

Example Question #3 : How To Find The Length Of The Diagonal Of A Hexagon

Example Question #4 : How To Find The Length Of The Diagonal Of A Hexagon

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: