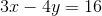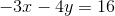Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : How to find the equation of a line

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find The Equation Of A Line

$\small \textup{Which is the equation of the line that passes through the points}$

$\small (1,2)\,\textup{and}\,(3.8)?$

Possible Answers:

$\small y=3x-1$

$\small y=\frac{x}{3}+1$

$\small y=-3x +2$

$\small y = x+5$

$\small y=3x+2$

Correct answer:

$\small y=3x-1$

Explanation:

Equation of line: $\small y = mx+b$ , $\small m$ = slope, $\small b$ = -intercept

Step 1) Find slope ( $\small m$ ): rise/run $\small \frac{8-2}{3-1}=\frac{6}{2}=3$

Step 2) Find -intercept ( $\small b$ ): $\small \frac{2-b}{1-0}=3$

$\small 2-b = 3$

$\small 2 = 3 + b$

$\small -1 =b$

$\small y=3x-1$

Report an Error

Example Question #12 : How To Find The Equation Of A Line

Whast line goes through the points (1,3) and (7,5) ?

Possible Answers:

4x+3y=7

x-2y=6

x+y=4

3x-2y=9

-x+3y=8

Correct answer:

-x+3y=8

Explanation:

Let $P_{1}=(1,3)$ and $P_{2}=(7,5)$

The slope is geven by: $m = (y_{2} - y_{1}) \div (x_{2} - x_{1})$ so

$m=\frac{1}{3}$

Then we use the slope-intercept form of an equation; y=mx+b so

$b=\frac{8}{3}$

And we convert

$y=\frac{1}{3}x+\frac{8}{3}$

to standard form.

Report an Error

Example Question #13 : How To Find The Equation Of A Line

What is the equation of the line that passes through the points (4,7) and (8,10)?

Possible Answers:

3x+4y=16

3x-4y=-16

3x-4y=16

-3x-4y=16

3x+4y=-16

Correct answer:

3x-4y=-16

Explanation:

In order to find the equation of the line, we will first need to find the slope between the two points through which it passes. The slope, , of a line that passes through the points (x_1,y_1) and (x_2,y_2) is given by the formula below:

$\text{slope}=m=\frac{y_2-y_1}{x_2-x_1}$

We are given our two points, (4,7) and (8,10), allowing us to calculate the slope.

$m=\frac{10-7}{8-4}=\frac{3}{4}$

Next, we can use point slope form to find the equation of a line with this slope that passes through one of the given points. We will use (4,7).

y-y_1=m(x-x_1)

$y-7=\frac{3}{4}(x-4)$

Multiply both sides by four to eliminate the fraction, and simplify by distribution.

$4(y-7)=4(\frac{3}{4})(x-4)$

4y-28=3(x-4)

4y-28=3x-12

Subtract from both sides and add twelve to both sides.

-28=3x-4y-12

-16=3x-4y

This gives our final answer: 3x-4y=-16

Report an Error

Example Question #14 : How To Find The Equation Of A Line

Which line contains the following ordered pairs:

$\left ( -2,4 \right )$ and $\left ( 6,2 \right )$

Possible Answers:

$\small y=-\frac{1}{4}x+\frac{7}{2}$

$\small y=-x+14$

$\small y=x+14$

$\small y=\frac{1}{4}x+\frac{7}{2}$

Correct answer:

$\small y=-\frac{1}{4}x+\frac{7}{2}$

Explanation:

First, solve for slope.

$\small m=\frac{\Delta y}{\Delta x}=\frac{2-4}{6-(-2)}=\frac{-2}{8}=-\frac{1}{4}$

Then, substitute one of the points into the equation y=mx+b.

$\small 2=(-\frac{1}{4})(6)+b$

$\small 2=(-\frac{3}{2})+b$

$\small b=2+\frac{3}{2}=\frac{7}{2}$

This leaves us with the equation $\small y=-\frac{1}{4}+\frac{7}{2}$

Report an Error

Example Question #24 : Slope And Line Equations

Axes

Refer to the above red line. What is its equation in standard form?

Possible Answers:

x + 3y = 6

3x + y = 18

3x - y = -18

x + 3y = - 6

x -3y = - 6

Correct answer:

3x - y = -18

Explanation:

First, we need to find the slope of the above line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18$ :

$m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3$

Second, we note that the -intercept is the point (0,18) .

Therefore, in the slope-intercept form of a line, we can set m = 3 and b = 18 :

y = mx+b

y = 3x + 18

Since we are looking for standard form - that is, Ax+By = C - we do the following:

y - y - 18 = 3x + 18 - y - 18

- 18 = 3x - y

3x - y = -18

Report an Error

Example Question #25 : Slope And Line Equations

Axes

Refer to the above red line. What is its equation in slope-intercept form?

Possible Answers:

$y = \frac{1}{3}x + 18$

y = 3x -6

y = 3x + 18

$y = \frac{1}{3}x -6$

$y = \frac{1}{3}x +6$

Correct answer:

y = 3x + 18

Explanation:

First, we need to find the slope of the above line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18$ :

$m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3$

Second, we note that the -intercept is the point (0,18) .

Therefore, in the slope-intercept form of a line, we can set m = 3 and b = 18 :

y = mx+b

y = 3x + 18

Report an Error

Example Question #26 : Psat Mathematics

Axes

Refer to the above red line. A line is drawn perpendicular to that line, and with the same -intercept. What is the equation of that line in slope-intercept form?

Possible Answers:

$y = -\frac{1}{3}x-6$

$y = \frac{1}{3}x-2$

$y = \frac{1}{3}x+6$

$y = -\frac{1}{3}x-2$

$y = -\frac{1}{3}x+6$

Correct answer:

$y = -\frac{1}{3}x-2$

Explanation:

First, we need to find the slope of the above line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18$ :

$m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3$

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 3, which is $m = -\frac{1}{3}$ .

Since we want the line to have the same -intercept as the above line, which is the point (-6,0) , we can use the slope-intercept form to help us. We set

$m = -\frac{1}{3},x= -6, y=0$ , and solve for in:

y = mx+b

$0 = -\frac{1}{3}(-6)+b$

0 =2 +b

b = -2

Substitute for and in the slope-intercept form, and the equation is

$y = -\frac{1}{3}x-2$

Report an Error

Example Question #15 : How To Find The Equation Of A Line

Find the equation of the line shown in the graph below:

Sat_math_164_05

Possible Answers:

y = 2x + 4

y = -1/2x + 4

y = -1/2x - 4

y = x/2 + 4

Correct answer:

y = x/2 + 4

Explanation:

Based on the graph the y-intercept is 4. So we can eliminate choice y = x/2 - 4.

The graph is rising to the right which means our slope is positive, so we can eliminate choice y = -1/2x + 4.

Based on the line, if we start at (0,4) and go up 1 then 2 to the right we will be back on the line, meaning we have a slope of (1/2).

Using the slope intercept formula we can plug in y= (1/2)x + 4.

Report an Error

View PSAT Mathematics Tutors

Tajrin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View PSAT Mathematics Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View PSAT Mathematics Tutors

Germaine
Certified Tutor

Princeton University, Bachelor in Arts, Philosophy.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Phoenix, ISEE Tutors in Dallas Fort Worth, Physics Tutors in Houston, SAT Tutors in San Diego, Biology Tutors in Denver, LSAT Tutors in Los Angeles, Algebra Tutors in Philadelphia, Chemistry Tutors in Los Angeles, French Tutors in Dallas Fort Worth, GMAT Tutors in Dallas Fort Worth

Popular Courses & Classes

LSAT Courses & Classes in Boston, LSAT Courses & Classes in New York City, LSAT Courses & Classes in Phoenix, LSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Chicago, ISEE Courses & Classes in Los Angeles, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Denver, ACT Courses & Classes in San Diego, GRE Courses & Classes in Washington DC

Popular Test Prep

GRE Test Prep in Los Angeles, ISEE Test Prep in Washington DC, SSAT Test Prep in New York City, MCAT Test Prep in San Diego, GMAT Test Prep in Philadelphia, GMAT Test Prep in Chicago, MCAT Test Prep in Boston, GRE Test Prep in Seattle, LSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : How to find the equation of a line

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #11 : How To Find The Equation Of A Line

Example Question #12 : How To Find The Equation Of A Line

Example Question #13 : How To Find The Equation Of A Line

Example Question #14 : How To Find The Equation Of A Line

Example Question #24 : Slope And Line Equations

Example Question #25 : Slope And Line Equations

Example Question #26 : Psat Mathematics

Example Question #15 : How To Find The Equation Of A Line

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: