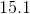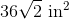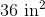The height of the pyramid is . The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:

The volume of a pyramid can be calculated using the fomula

The volume of a tetrahedron is found with the equation , where  represents the length of an edge of the tetrahedron.

Plug in 4 for the edge length and reduce as much as possible to find the answer:

The volume of the tetrahedron is .

The area of an equilateral triangle is given by the formula

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is 

Substitute :

 square inches.

The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

The total surface area is four times this, or about .

Rounded, this is 84.9.

First we write out the equation we are given. H + (2L +2W) = 360.  H = 40 and L = 23

40 + (2(23) + 2W) = 360

40 + (46 + 2W) = 360

46 + 2W = 320

2W = 274

W = 137

Method 1:

Trial and error to find a combination of factors of 80 that differ by the same amount will eventually yield 2, 5, 8.  The average is 5.

Method 2:

Three terms of an arithmetic sequence can be written as x, x+d, and x+2d. Multiply these together using the distributive property to find the volume and the following equation results:

x³ + 3dx² + 2d²x - 80 = 0

Find an integer value of x that creates an integer solution for d.  Try x=1 and we see the equation 1 + 3d + 2d² - 80 = 0 or 2d² + 3d -79 = 0.  The determinant of this quadratic is 641, which is not a perfect square.  Therefore, d is not an integer when x=1.

Try x=2 and we see the equation 8 + 12d + 4d² - 80 = 0 or d² + 3d - 18 = 0.  This is easily factored to (d+6)(d-3)=0 so d=-6 or d=3.  Since a negative value of d will result in negative dimensions of the prism, d must equal 3.  Therefore, when substituting x=2 and d=3, the dimensions x, x+d, and x+2d become 2, 5, and 8.  The average is 5.

Based on our prompt, we can say that the prism has dimensions that can be represented as:

Dim1: x

Dim2: 2 * Dim1 = 2x

Dim3: (1/4) * Dim2 = (1/4) * 2x = (1/2) * x

More directly stated, therefore, our dimensions are: x, 2x, and 0.5x. Therefore, the volume is x * 2x * 0.5x = 64, which simplifies to x³ = 64. Solving for x, we find x = 4. Therefore, our dimensions are:

x = 4

2x = 8

0.5x = 2

Or: 2 x 4 x 8

Based on our prompt, we can say that the prism has dimensions that can be represented as:

Dim1: x

Dim2: 3 * Dim1 = 3x

Dim3: 5 * Dim1 = 5x

More directly stated, therefore, our dimensions are: x, 3x, and 5x. Therefore, the volume is x * 3x * 5x = 120, which simplifies to 15x³ = 120 or x³ = 8. Solving for x, we find x = 2. Therefore, our dimensions are:

x = 2

3x = 6

5x = 10

Or: 2 x 6 x 10

In order to figure out how many cubic centimeters can fit into the box, we need to figure out the volume of the box in terms of cubic centimeters. However, the measurements of the box are given in meters. Therefore, we need to convert these measurements to centimeters and then determine the volume of the box.

There are 100 centimeters in one meter. This means that in order to convert from meters to centimeters, we must multiply by 100.

The length of the box is 2 meters, which is equal to 2 x 100, or 200, centimeters.

The width of the box is 0.5(100) = 50 centimeters.

The height of the box is 3.2(100) = 320 centimeters.

Now that all of our measurements are in centimeters, we can calculate the volume of the box in cubic centimeters. Remember that the volume of a rectangular box (or prism) is equal to the product of the length, width, and height.

V = length x width x height

V = (200 cm)(50 cm)(320 cm) = 3,200,000 cm³

To rewrite this in scientific notation, we must move the decimal six places to the left.

V = 3.2 x 10⁶ cm³

The answer is 3.2 x 10⁶.

Let l be the length, w be the width, and h be the height of the prism. We are told that the length is twice the width, and that the width is twice the height. We can set up the following two equations:

l = 2w

w = 2h

Next, we are told that the surface area is equal to 252 square units. Using the formula for the surface area of the rectangular prism, we can write the following equation:

surface area = 2lw + 2lh + 2wh = 252

We now have three equations and three unknowns. In order to solve for one of the variables, let's try to write w and l in terms of h. We know that w = 2h. Because l = 2w, we can write l as follows:

l = 2w = 2(2h) = 4h

Now, let's substitute w = 2h and l = 4h into the equation we wrote for surface area.

2(4h)(2h) + 2(4h)(h) + 2(2h)(h) = 252

Simplify each term.

16h² + 8h² + 4h² = 252

Combine h² terms.

28h² = 252

Divide both sides by 28.

h² = 9

Take the square root of both sides.

h = 3.

This means that h = 3. Because w = 2h, the width must be 6. And because l = 2w, the length must be 12.

Because we now know the length, width, and height, we can find the volume of the prism, which is what the question ultimately requires us to find.

volume of a prism = l • w • h

volume = 12(6)(3)

= 216 cubic units

The answer is 216.